Sobald der Mensch reisen möchte, sei es zu Fuß, zu Pferd, mit dem Auto, mit dem Boot oder mit dem Flugzeug, stellt sich zunächst das Problem, die Route zu wählen, der er folgen möchte. Nicht sehr kompliziert, wenn die Reise kurz ist, man das Gelände gut kennt und über zahlreiche Anhaltspunkte verfügt. Das Problem wird noch komplizierter, wenn wir sehr weit reisen wollen, einen Ozean oder eine Wüste überqueren, wenn es Nacht ist oder wir über einer Wolkenschicht fliegen. Das ist der ganze Zweck der Navigation, dessen Grundlagen wir hier untersuchen werden…

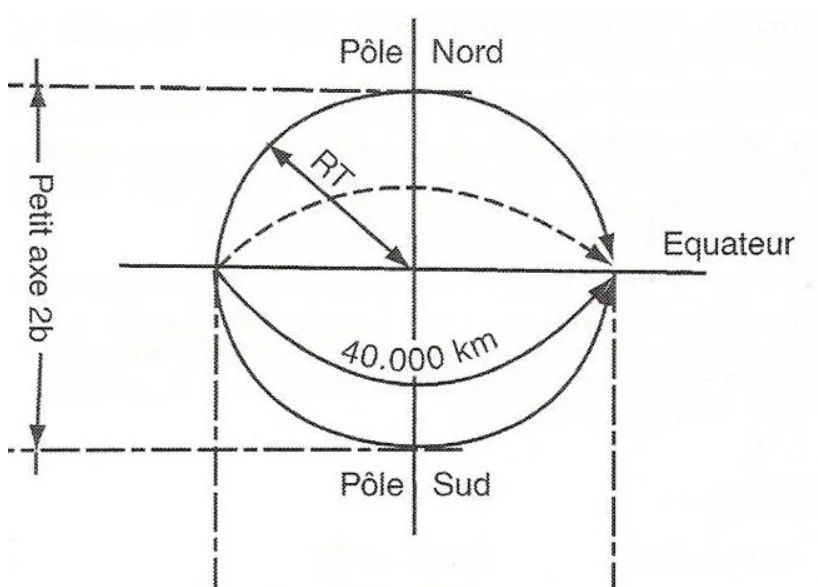
Unsere Erde ist ein Rotationsellipsoid, vergleichbar vereinfacht gesagt einer Kugel mit einem mittleren Radius von 6337 km. Der Unterschied zwischen der Nebenachse und der Hauptachse beträgt etwa 22 km, der durchschnittliche Umfang liegt bei knapp 40.000 km.

Die Erde dreht sich in 24 Stunden um sich selbst, um ihre Nord-Süd-Achse und in 365 Tagen um die Sonne. Die Achse der Pole ist um 23°27' gegenüber der Ebene der Ekliptik geneigt, die den Ursprung der Jahreszeiten darstellt.

Um die Positionsbestimmung zu ermöglichen, wurden unterschiedliche Systeme entwickelt. Am bekanntesten und gebräuchlichsten ist der, der die Erde dank des Äquators in zwei Hemisphären teilt. Parallel zu diesem Äquator liegen Parallelen, die den Breitengrad L definieren. Er wird von 0° bis 90° nach Norden oder nach Süden gezählt.

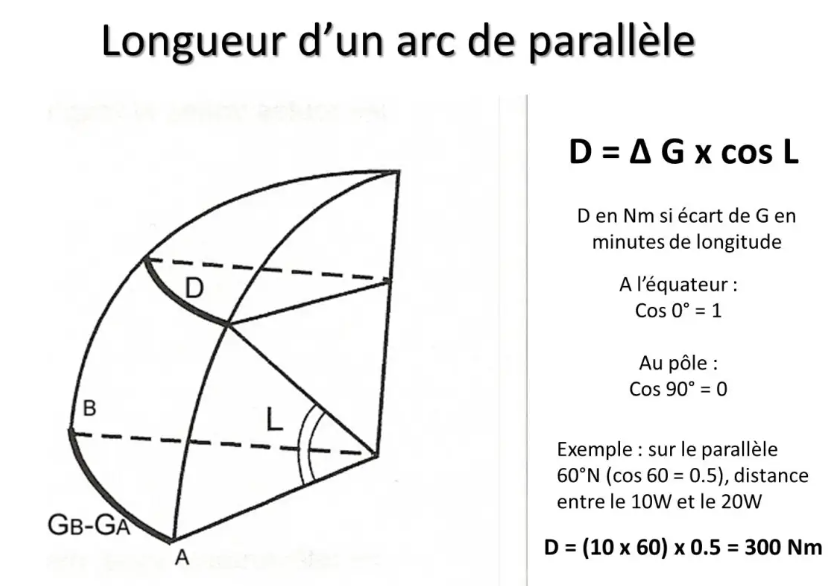
Für Mathematiker und ohne auf eine komplexe mathematische Demonstration einzugehen: Wenn wir uns einfach daran erinnern, dass der Kosinus der Breite von 1 auf 0 abnimmt, wenn er von 0° auf 90° zunimmt, werden wir uns intuitiv daran erinnern, dass die Länge eines Parallelbogens entsprechend variiert zum Kosinus seines Breitengrades…

L'ESTIME (Koppelnavigation)

Dies ist die Grundlage jeder Navigation. Und das ist auch heute noch relevant, da die modernsten Navigationsmittel nichts weiter leisten als mit der großen Präzision, die die aktuelle Technologie ermöglicht. Wir werden noch einmal darüber sprechen, wenn wir uns diese Tools ansehen.

Was auch immer unser Transportmittel ist: Um von Punkt A zu Punkt B zu gelangen, müssen wir zunächst unser Fahrzeug lenken oder in Richtung Punkt B lenken. Dies ist das Wichtigste, aber nicht unbedingt das Einfachste: Erinnern wir uns an Christoph Kolumbus, der nach Westen fuhr, um dorthin zu gelangen nach Indien...!



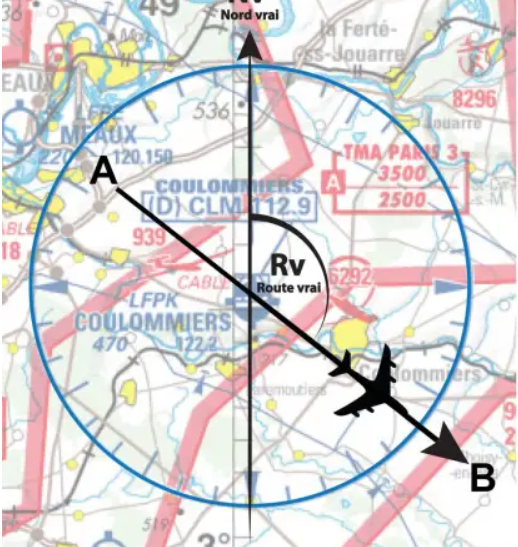
Wir müssen daher sagen können, in welcher Richtung sich B befindet und in Bezug auf welche Referenz, im Allgemeinen die Richtung des Nordpols. Dies ist der wahre Kurswinkel Rv, ausgedrückt in Grad relativ zu Nv im Uhrzeigersinn.

Wenn wir B von A sehen, ist das einfach, aber selten! Wir können von sichtbarem Punkt zu sichtbarem Punkt fliegen, das machen wir im Sichtflug. Ist dies nicht möglich oder möchten Sie die Navigation visuell kontrollieren, müssen Sie diese auf einer Karte ausmessen oder berechnen...

Dann müssen Sie die Distanz kennen, die Sie zurücklegen müssen, um Punkt B oder einen Zwischenpunkt zu erreichen, falls einer definiert wurde. Wir können dann die Flugzeit für diese Reise abschätzen, indem wir diese Distanz durch die Geschwindigkeit relativ zum Boden dividieren.

Der Kurswinkel Rv und die Reisezeit werden die beiden Elemente sein, die es uns ermöglichen, „durch Koppelnavigation“ zu navigieren. Wir sagen auch „Kopf und Wache“.

Zu den am häufigsten verwendeten Mitteln zur Bestimmung der beiden Elemente der Koppelnavigation, nämlich Kurswinkel und Entfernung, gehören natürlich Karten.

KARTOGRAPHIE

Viele Gründe, darunter auch die Navigation, führten dazu, dass man die Erde darstellen wollte. Aber es ist sehr schwierig, es getreu zu machen, insbesondere wegen seiner nicht sehr… katholischen Form (vgl. Galileo und Kopernikus)!

Die getreueste Darstellung ist die Weltkarte: offensichtlich sehr groß und für die Verwendung im Flugzeug wirklich nicht praktikabel!!!

Allgemein

Bei Karten ist die Darstellung eines annähernd kugelförmigen Objekts auf einem flachen Blatt Papier nicht mit Präzision möglich: Daher müssen Kompromisse eingegangen werden und die Elemente ausgewählt werden, die originalgetreu wiedergegeben werden sollen, zum Nachteil anderer Elemente, die weniger originalgetreu oder überhaupt nicht wiedergegeben werden . überhaupt !

Einer der wichtigsten Punkte für die Navigation ist, wie wir gerade gesehen haben, die Ausrichtung der Flugbahn mit dem Straßenwinkel Rv.

Konformität



Wir müssen daher in der Lage sein, die Winkel genau zu messen: das nennen wir Konformität. Wenn sich auf einer konformen Karte zwei Linien auf der Erde in einem Winkel von 47° schneiden, schneiden sich ihre Darstellungen auf der Karte ebenfalls in einem Winkel von 47°. Die Winkel bleiben somit erhalten.

Damit eine Karte konform ist, muss der Maßstab um einen bestimmten Punkt auf der Karte in alle Richtungen konstant sein, insbesondere in den beiden senkrechten Richtungen, den Meridianen und Parallelen.

Warum ist es so wichtig, Winkel genau zu messen?

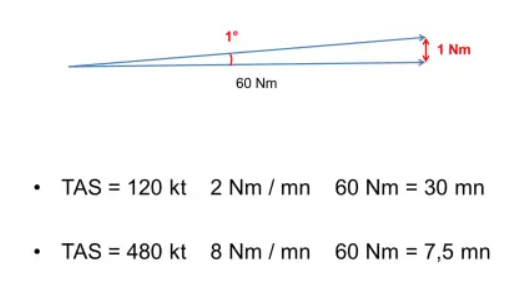
Bei nur einem kleinen Fehler beträgt die Abweichung nach 60 Nm 1 Nm von der Fahrbahn! Und 60 Nm sind 30 Minuten im C172, aber kaum 8 Minuten für einen Jet im Reiseflug! Und es gibt mehrere Fehlerquellen: Messung, Fehler des Navigationsinstruments, Winddrift usw.

Die richtige Karte

Dann wäre es gut, wenn wir durch das Zeichnen einer Linie auf der Karte mit einem Lineal die Flugbahn definieren würden, der wir folgen möchten, sei es eine orthodrome Linie, eine Loxodrome oder eine andere „Dromie“, darauf kommen wir zurück.

Äquidistanz

Und schließlich, um Entfernungen zu messen: Wenn der Maßstab auf der gesamten Karte konstant wäre (wir würden dann sagen, dass er äquidistant ist), wäre das perfekt! Tatsächlich stellt dies, wie wir gerade gesehen haben, kein großes Problem dar, wenn man bedenkt, dass wir eine Entfernung immer messen können, indem wir sie auf dem nächstgelegenen Meridian eintragen und die Breitengradminuten, also Seemeilen, zählen!

Es ist unmöglich, diese drei Eigenschaften genau zu erfüllen: Die Luftfahrtkarten werden daher zunächst konform sein. Im Übrigen müssen Sie den am besten geeigneten Kompromiss wählen.



BEI CARTE MERCATOR

Es wurde 1569 von Gerardus Mercator entwickelt, der ihm seinen Namen gab, und ist sicherlich die bekannteste Darstellung der Welt.

Merkmale

Es handelt sich um eine zylindrische Projektion tangential zum Äquator. Es handelt sich jedoch nicht um eine geometrische Projektion: Der Abstand der Parallelen wird mathematisch berechnet, sodass die Karte konform und daher in der Navigation verwendbar ist (zunehmende Breitengrade, Grundelement von 1/cos L).

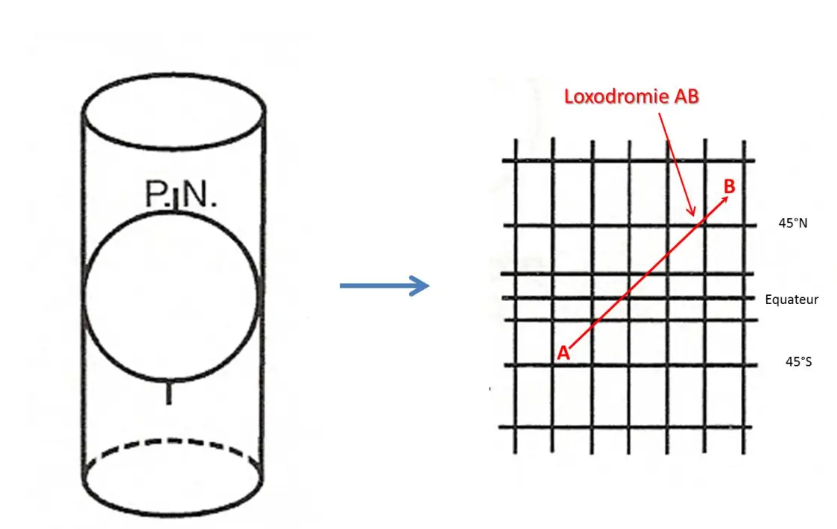
Die Parallelen und Meridiane werden durch zueinander senkrechte Geraden dargestellt: Dies ist sehr praktisch für die Navigation mit konstantem Kurs, denn wenn wir eine Linie auf der Karte zeichnen, ist der Rv auf der gesamten Route gleich: Die so verfolgte Route wird a genannt Rhumb-Linie.

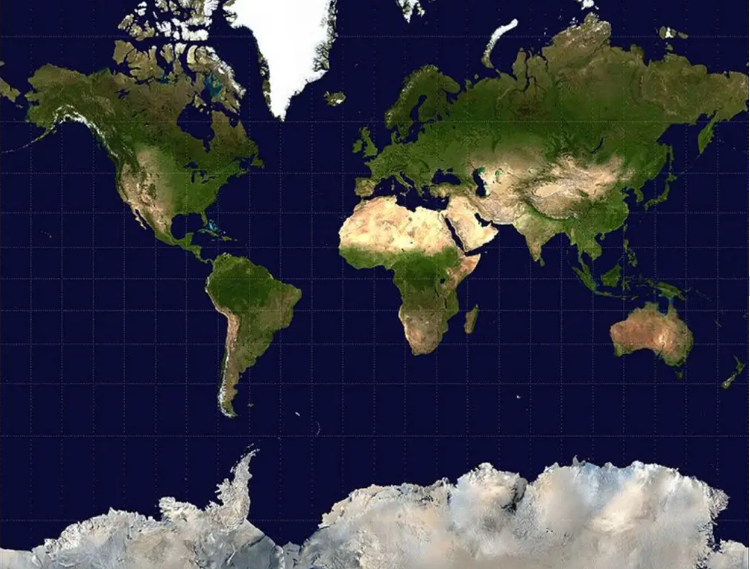
Der Maßstab hingegen ist sehr variabel, was die Flächen erheblich verzerrt: Grönland erscheint mit seinen 2 Millionen km² so groß wie ganz Afrika, das etwa 15-mal größer ist!!!

Der Maßstab ist am Äquator minimal und nimmt zu den Polen hin zu.

Es ist nicht möglich, die Polarzonen auf einer Mercator-Karte darzustellen.

Die auf den Planisphären der Fluggesellschaften dargestellte Route von Paris nach San Francisco bildet eine wunderschöne Schleife über Grönland und die Hudson Bay in Kanada, während die gerade Linie über New York verlaufen würde??? Diejenigen, die die Gelegenheit hatten, an die Westküste der USA zu fliegen, können bestätigen, dass wir tatsächlich über den großen Norden fliegen.

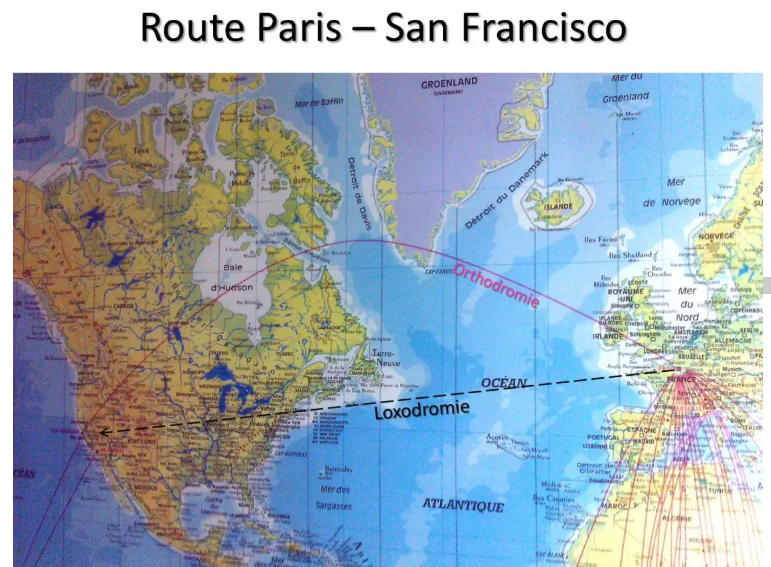
Tatsächlich ist die Rhumb-Linie nicht der direkteste Weg: Die gerade Linie auf unserer kugelförmigen Erde ist in Wirklichkeit ein Bogen eines Großkreises (dessen Mittelpunkt der der Erde ist), der durch unsere beiden Punkte A und B verläuft. Denn zu haben Bestätigung, auf einer Weltkarte, indem wir einen Draht zwischen Paris und San Francisco spannen, werden wir den kürzesten Weg verwirklichen. Dies wird als Orthodromie bezeichnet.

Um Ihnen eine Vorstellung zu geben: Der Großkreisabstand zwischen CDG und SFO beträgt 4836 Nm, während der loxodromische Abstand etwa 5600 Nm beträgt: 800 Nm, der Unterschied ist nicht gering!!!

Die präzise Erstellung einer Mercator-Karte ist eine Sache für Profis: Vielen Dank, IGN. Andererseits können wir einen kleinen Ausschnitt davon auch grafisch leicht konstruieren.



Erstellen einer Mercator-Karte

Um dies zu veranschaulichen, biete ich Ihnen eine kleine praktische Übung an:

Stellen wir uns vor, Sie erben von Ihrer Großmutter eine schöne Summe Geld und ein großes Stück Land im Südwesten, etwa 45° N und 1° 30 E. Mit dem Geld entscheiden Sie sich für den Kauf eines Ultraleichtflugzeugs und mit dem Gelände dazu Erstellen Sie einen Track, um ihn zu verwenden. Sie möchten ihn zur VAC-Karte machen, um sowohl die QFU und die Länge des Tracks zu kennen als auch ihn anderen Benutzern bekannt zu machen.

Zeichnen Sie zunächst ein Rechteck mit einer Höhe von 12 cm und einer Breite von 14 cm. Die vertikalen Seiten sind die Meridiane, die horizontalen die Parallelen unserer Mercator-Karte.

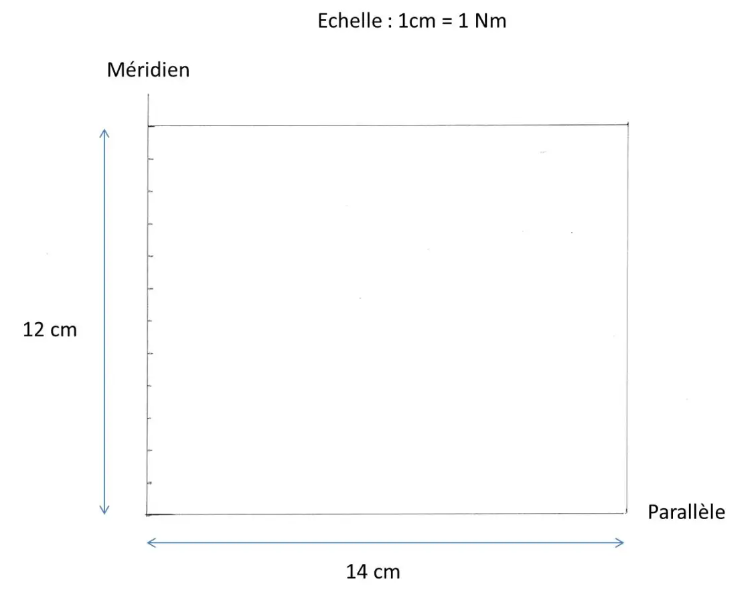
Skalieren Sie die linke vertikale Seite von cm auf cm. Wir legen den Maßstab fest: 1 cm = 1 Nm.

Zeichnen Sie eine Linie, die von der unteren linken Ecke ausgeht und einen Winkel von 45°, dem Breitengrad unseres Landes, mit der unteren Parallele bildet. Wir können dies auch tun, indem wir die Diagonale eines Quadrats zeichnen ...

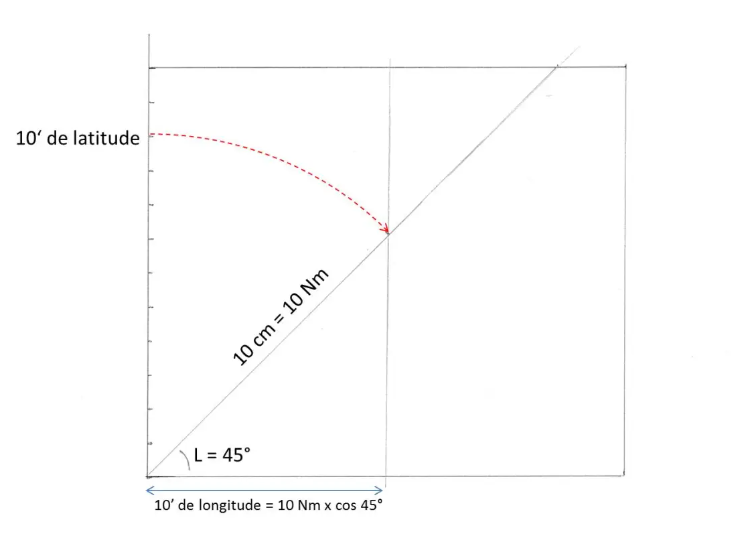
Übertragen Sie auf dieser Linie den 10-cm-Meridian, der 10 Minuten Breite entspricht, also 10 Nm. Senken Sie eine vertikale Linie auf die untere Parallele. Wir haben gerade die Länge eines Segments von 10 Längengraden abgegrenzt: Wie wir oben gesehen haben, misst es 10 x cos 45° oder etwa 7 Nm, also 7 cm auf unserer Karte. (cos 45° = 0,707, wie der Sinus der aerodynamischste der Sinus!!!).

Der Maßstab ist daher auf dem Meridian und dem Parallelen gleich: Unsere Leinwand ist daher konsistent!

Sie verstehen besser, warum ich ein Rechteck mit einer Breite von 14 cm gewählt habe, das also 20 Längenminuten entspricht.

Es bleibt nur noch, unsere Längengradskala alle 7 mm zu unterteilen.

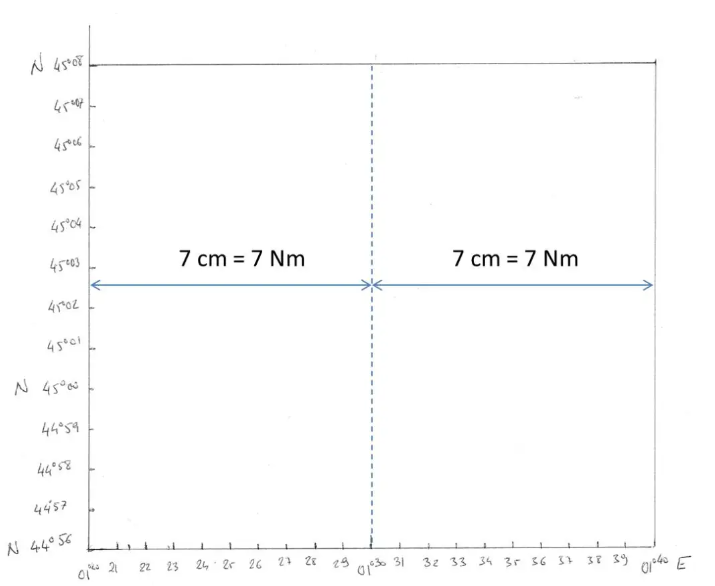
Damit unsere Spur ungefähr zentriert ist, verschlüsseln wir die Breitengrade von 44°56' bis 45°58'N und die Längengrade von 001°20' bis 001°40'E.

Wir haben gerade eine konsistente Leinwand erstellt (gleicher Maßstab auf den Meridianen und Parallelen). Es handelt sich um eine Mercator-Leinwand, da die Meridiane und Parallelen senkrechte Linien sind!!!



Mit Ihrem GPS haben Sie die Position der beiden QFUs gemessen: NW: 45°02,6 N und 001°28,3 E und SE 45°02,2 N und 001°29,8 E. Jetzt müssen Sie sie nur noch auf unserer Karte positionieren .

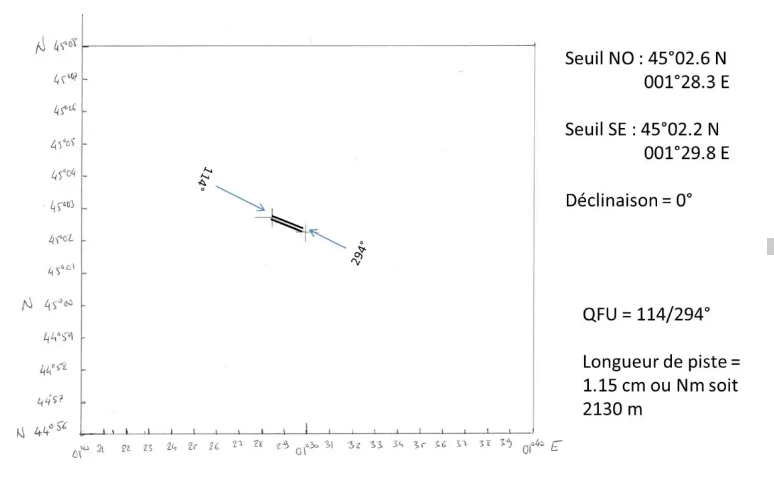
Mit einem Winkelmesser kann man nun die QFU messen, und mit einem Doppeldezimeter die Länge der Strecke: Ich für meinen Teil habe die QFU 114°/294° und eine Schienenlänge von 1,15 cm ermittelt, also 1,15 Nm, also 2130 m .

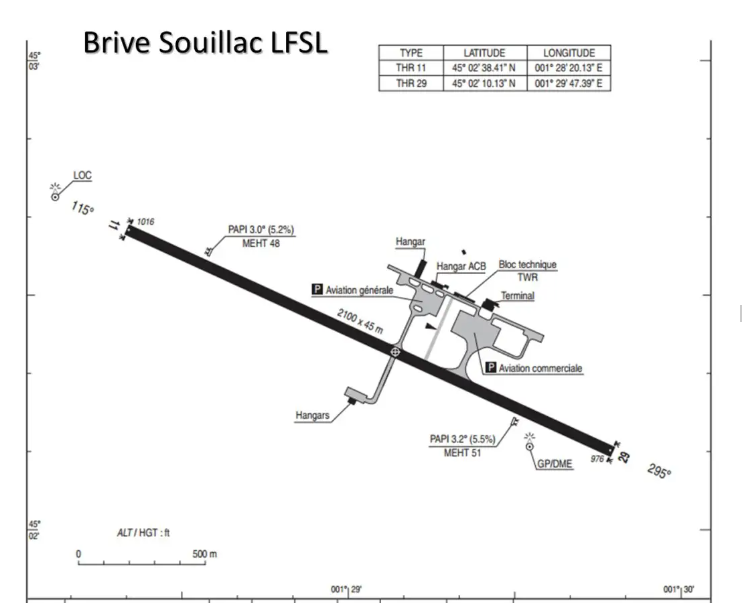
Wenn Sie ein wenig in den SIA-Akten stöbern, werden Sie leicht feststellen, dass Ihre Großmutter Ihnen tatsächlich das Land Brive Souillac hinterlassen hat, dessen QFU 115°/295° beträgt und die Landebahnlänge 2100 m beträgt!!!



In der Luftfahrt

Die Mercator-Projektion wird selten für Luftfahrtnavigationskarten verwendet. Nur äquatoriale Regionen ermöglichen natürlich eine Karte, die sowohl konform als auch praktisch orthodromal und äquidistant ist, da sie nahe am Äquator liegt.

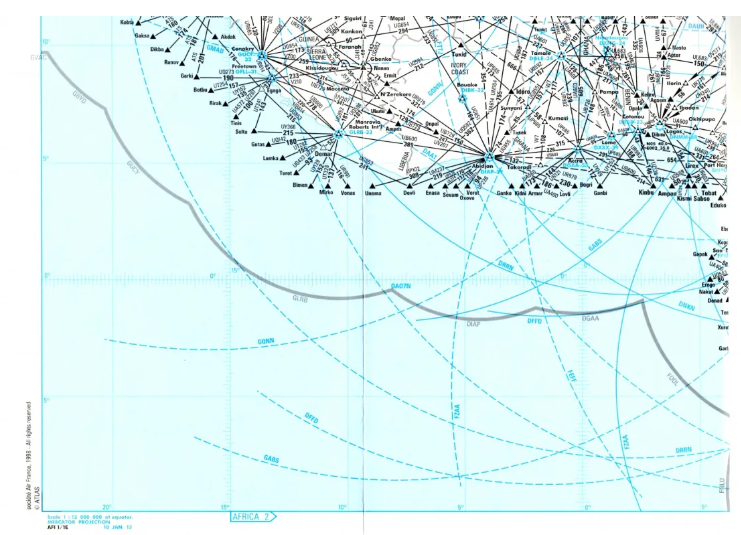
Diese AFRIKA-1-Straßenkarte für die ETOPS-Flugplanung ist eine davon, obwohl es sich nicht wirklich um eine Navigationskarte handelt (zum Vergrößern anklicken).

DIE LAMBERT-KARTE

Einer der Hauptfehler der Mercator-Karte besteht darin, dass die gerade Linie auf der Karte nicht die gerade Linie auf der Erde darstellt. Aber es gibt Lösungen … die erste heißt Lambert-Karte.



Merkmale

Es handelt sich um eine konforme konische Projektion, die Ende des 18. Jahrhunderts vom elsässischen Mathematiker Johann Henrich Lambert vorgestellt wurde und die Erdkugel entlang einer Parallele tangiert. Wie bei der Mercator-Karte handelt es sich nicht um eine geometrische Projektion, sondern um eine mathematische Konstruktion.

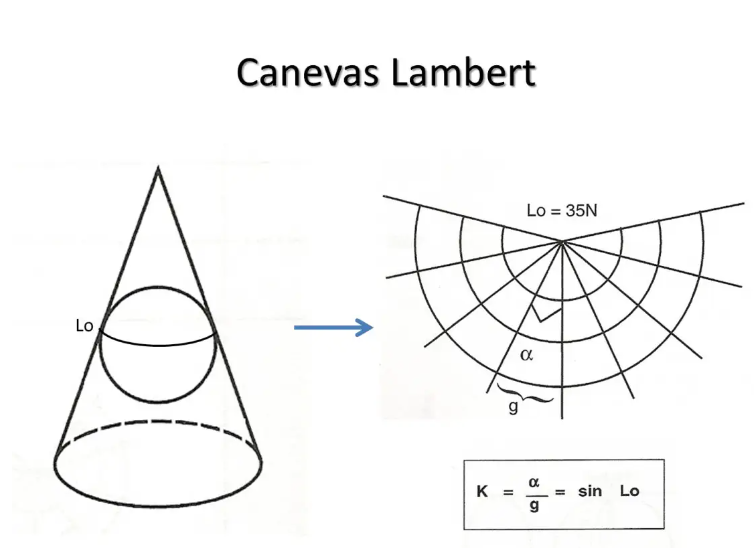
Die Meridiane werden durch gerade Linien dargestellt, die zum Pol hin zusammenlaufen. Den Konvergenzfaktor K nennen wir das Verhältnis zwischen dem Winkel, den zwei Meridiane auf der Karte bilden, und dem Winkel, den sie auf der Erde bilden. Wenn die Tangentialparallele den Breitengrad Lo hat, ist der Faktor K = sin Lo.

Parallelen werden durch konzentrische Kreise dargestellt.

Wie alle konformen Karten ist dieser Kartentyp in der Nähe der Tangentialparallele praktisch orthodromisch, das heißt, die gerade Karte ist praktisch die Darstellung einer Orthodromatik. Die Mercator-Karte ist tatsächlich ein Sonderfall der Lambert-Karte, bei der die Tangentenparallele der Äquator ist! In der Nähe des Äquators wird es daher orthodromal sein.

Um eine orthodrome Lambert-Karte zu erhalten, reicht es daher aus, eine Tangentialparallele zu wählen, deren Mittelpunkt auf dem Bereich liegt, den Sie darstellen möchten …

Wie bei der Mercator-Karte ist der Maßstab am Tangentialparallel Lo minimal und nimmt deutlich zu, wenn wir uns davon entfernen.

Um diesen Nachteil zu beheben, wurden sogenannte „Sekanten“-Lambert-Kegelkarten erstellt. Der offizielle Maßstab der Karte ist nur auf der Ebene zweier Parallelen real, die sich auf beiden Seiten des Tangentialparallelen befinden. Das läuft darauf hinaus, dass der Projektionskegel die Erdoberfläche entlang dieser beiden sogenannten „Standard“- oder „konservierten Maßstabsparallelen“ schneidet. Der Maßstab ist zwischen diesen beiden Parallelen etwas kleiner und darüber hinaus etwas größer, was eine praktisch gleichgroße Leinwand über eine größere Fläche ergibt!

Der Faktor K ist dann der Sinus der mittleren Breite zwischen den beiden Standardparallelen oder ungefähr, weil die Maßstabsänderung auf beiden Seiten der Tangentialparallele nicht symmetrisch ist.

Die meisten Luftfahrtkarten, die in unseren Regionen mittlerer Breite verwendet werden, sind von diesem Typ. So können wir auf der vom IGN veröffentlichten VFR-Karte im Maßstab 1:500.000 des Nordwestens Frankreichs lesen: „Lambert-konforme konische Projektion. Parallelen im erhaltenen Maßstab 45°54' und 47°42'" (die Standardparallelen).

Daraus ergibt sich ein mittlerer Breitengrad Lo = 46°48' N und damit ein Faktor K = 0,728.

In der Luftfahrt

Hier ist zum Beispiel ein Auszug aus dem ATLAS 55C-Lastwagen, der für Nordatlantiküberquerungen (hier ein Flug Paris-New York) eingesetzt wird und dessen Standardparallelen 37° und 65° N sind (zum Vergrößern anklicken).

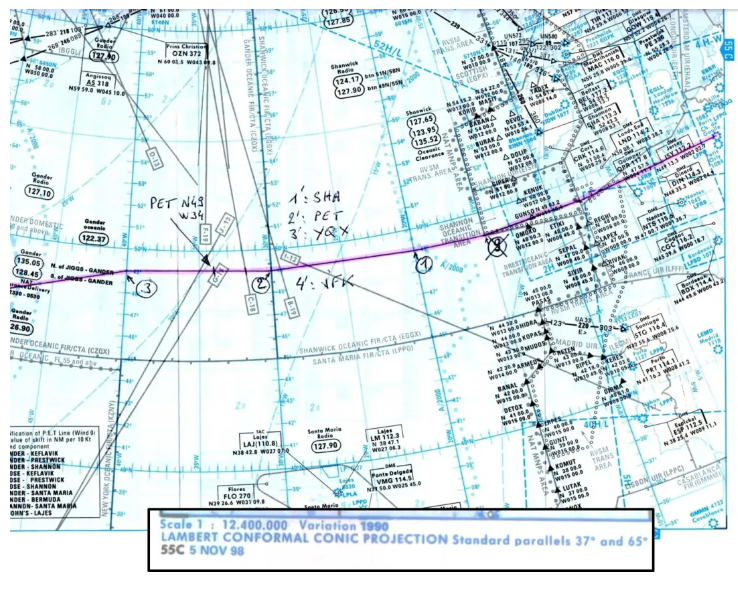
Wir können deutlich die Meridiane erkennen, die durch gerade Linien dargestellt werden und zum Nordpol hin zusammenlaufen, und die Parallelkreise, die durch konzentrische Kreise dargestellt werden.

Mit dieser Art von Karte kommen wir der perfekten Karte sehr nahe: Sie ist im dargestellten Gebiet einheitlich, um Routen oder Peilungen genau zu messen, orthodromisch, um kürzeste Routen mit einem Lineal nachzuzeichnen, und praktisch äquidistant, da der Maßstab kaum variiert: die Heilige Gral des Kartographen!

Kurioserweise handelt es sich bei der SIA-Karte „En Route“ (obwohl nicht angegeben) um eine Mercator-Karte, die anhand ihrer parallelen Meridiane leicht zu überprüfen ist, während sie Luftwege darstellt, die durch VOR-Radiale definiert sind, bei denen es sich um Orthodromien handelt.

*

Welche Art von Karte?

Um dieses Kapitel zu schließen: Versuchen wir herauszufinden, welche Art von Leinwand von der SIA zur Darstellung der SIDs und STARs verwendet wird: Nehmen wir zum Beispiel eine der LFPG-SID-Karten.

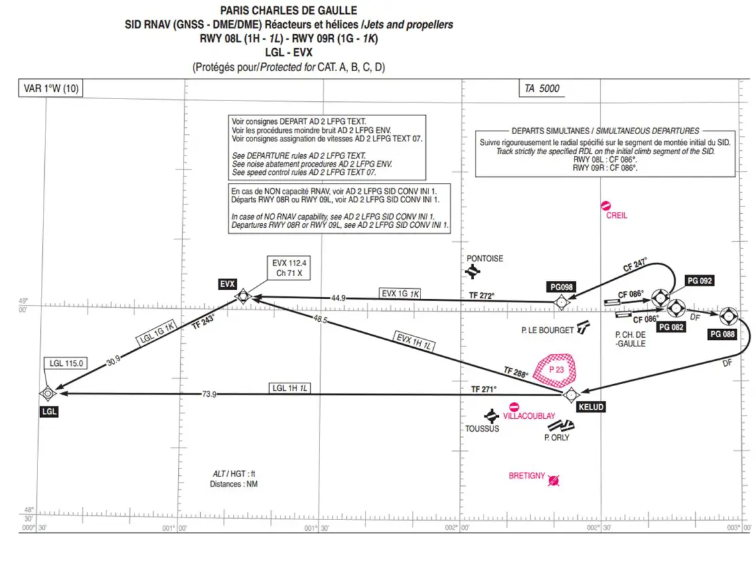
Mit einem Lineal oder durch Annäherung an eine Parallele zum Bildschirmrand erkennen wir, dass es sich bei den dargestellten Parallelen nicht um Geraden handelt. Und indem wir den Abstand zwischen zwei Meridianen oben und unten messen, sehen wir, dass sie nicht parallel sind.

Es handelt sich also sicherlich nicht um eine Mercator-Leinwand, sicherlich Lambert, aber die geringe Größe des dargestellten Stücks ermöglicht es nicht, den Winkel zwischen zwei Meridianen zu messen, der mit ihrem Längengradunterschied verglichen werden müsste, um den Faktor K und damit die Tangentialparallele zu bestimmen …

Weitere Informationen zu den in Frankreich verwendeten Lambert-Karten finden Sie auf der Wikipedia-Seite zu Lambert-Karten:

https://fr.wikipedia.org/wiki/Projection_conique_conforme_de_Lambert

ANDERE KARTENARTEN

Mit der Mercator-Karte für die Äquatorregion und der Lambert-Karte für die anderen Breitengrade haben wir fast alle Probleme gelöst. Es gibt noch einige Sonderfälle, die zur Erfindung (ganz) besonderer Karten führten.

Die polare stereografische Karte

Der erste dieser Fälle ist eine Karte, die zur Darstellung der Polarregionen erstellt wurde: Dies wird als polare stereografische Leinwand bezeichnet. Es ist eine Projektion auf eine Ebene tangential zum Pol. Und dieses Mal konnten wir es wirklich durch geometrische Projektion vom Gegenpol konstruieren.

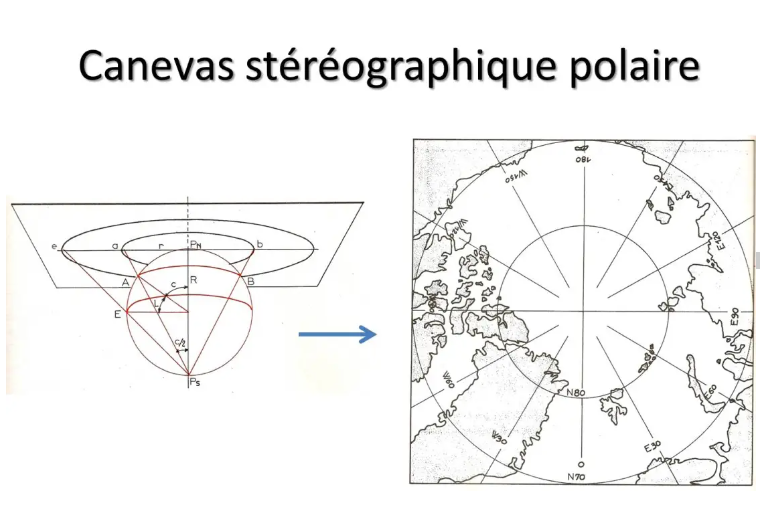
Dadurch erhalten wir eine Karte, auf der alle Meridiane durch gerade Linien dargestellt werden, die vom Pol in Form einer 360°-Rose beginnen. Parallelen sind konzentrische Kreise.

Selbstverständlich ist diese Karte für die Navigation geeignet. In der Nähe seines Tangentialpunktes, dem Pol, ist es orthodromal.

Der Maßstab ist an der Stange minimal und nimmt von Ihnen weg zu.

Der Einsatz beschränkt sich daher auf die Darstellung von Polargebieten und zugehörigen Routen. Hier ein Auszug aus dem Polartourenfahrzeug ATLAS 90C:

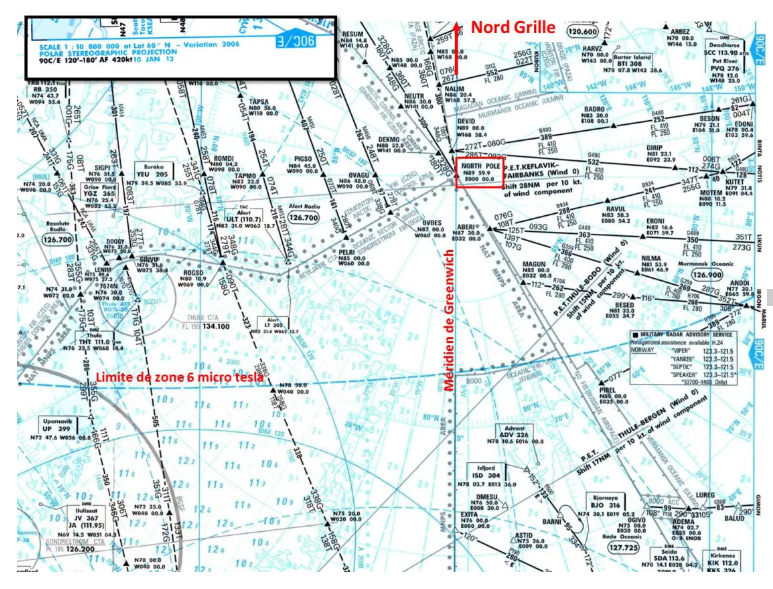
Die sehr starke Konvergenz der Meridiane und die Unzuverlässigkeit von Magnetkompassen in den Polarregionen (Zone 6 Mikrotesla) machen es sehr schwierig, einer Route mit konstantem Kurs zu folgen. Zu diesem Zweck verfügt die Karte über ein Raster, das an einem Nordgitter ausgerichtet ist, um auf einem konstanten Routengitter Rg zu navigieren.

In der Vergangenheit wurden auch andere Arten von Leinwänden erdacht und verwendet.

Die Transverse Mercator-Karte

Basierend auf der Idee, dass der Äquator ein großer Kreis ist, wurden sogenannte transversale Mercator-Karten nach dem gleichen Prinzip wie die direkte Mercator-Projektion, einer zylindrischen Projektion, entworfen, haben aber als „Äquator“ den Greenwich-Meridian und den 180°-Meridian (wir können tun Sie dies auch entsprechend einem beliebigen Meridianpaar und seinem Antimeridian).

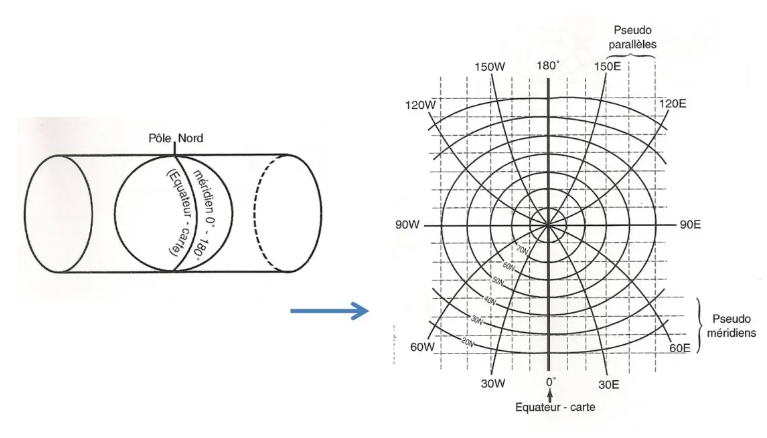
Dies ergibt eine Leinwand, die natürlich konform und orthodromal auf jeder Seite ihres Kartenäquators ist, der auch der einzige ist, der durch eine gerade Linie dargestellt wird. Daher ist es zwingend erforderlich, ein Raster mit „Pseudo-Parallelen“ und „Pseudo-Meridianen“ zu verwenden…

Auf diesem Modell wurde die Air-France-Karte „Frankreich-Alaska“ erstellt, die vor der Einführung der Trägheitsnavigationssysteme INS und während des Kalten Krieges, einer Zeit, in der das Überfliegen Sibiriens verboten war, verwendet wurde. Die kürzeste Route nach Japan führte durch der Nordpolregion.

Die Verwendung ist professionellen Navigatoren vorbehalten, da sie eher schwierig zu handhaben sind…!

Die Oblique Mercator-Karte

Noch stärker: Warum nicht eine Mercator-Karte mit einem Großkreis als Kartenäquator erstellen?

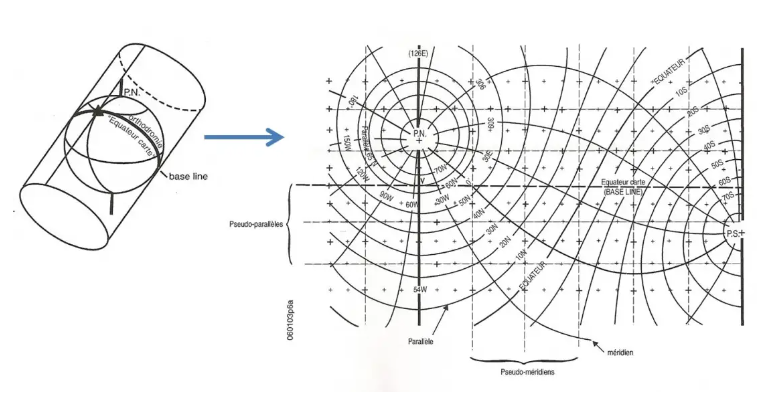
Dies wird als Oblique Mercator-Karte bezeichnet und ist noch weniger einfach zu verwenden!!!

ORTHODROMIE ODER LOXODROMIE?

Wie wir oben gesehen haben, gibt es zwischen einem Punkt A und einem Punkt B mindestens zwei mögliche Flugbahnen: die Loxodrome und den Großkreis.

Welches soll ich wählen?

Es wird von verschiedenen Elementen abhängen und vor allem von den Navigationsmitteln, die wir nutzen können.

Mit dem einfachsten Kompass, dem Magnetkompass, können Sie den Rhumb-Linien mit konstantem Kurs folgen, vorausgesetzt natürlich, Sie wissen, wie Sie Abweichungen, Deklinationen und Drift korrigieren. Wir werden in einem Artikel über Navigationsmethoden noch einmal darüber sprechen.

Wie wir auch in diesem Artikel sehen werden, folgen moderne Mittel Großkreisen ... Andererseits ist es nicht ganz einfach, einem Großkreis mit einem Kompass zu folgen, da sich der Rv ständig ändert. Und moderne Navigationsmittel können nicht einer Kompasslinie folgen!

Aber ist es sehr wichtig, den Unterschied zu machen?

Erstens gibt es einige Fälle, in denen die beiden verwechselt werden: Der Äquator ist sowohl ein Ortho als auch ein Loxo. Ebenso sind die Meridiane Orthos (halbe große Kreise), aber auch Loxos, da wir ihnen mit konstantem Rv, 180° oder 360°, folgen!

Der allgemeine Fall bleibt bestehen. Nehmen wir gleich an, dass der Unterschied auf Abschnitten von einigen zehn Nm, wie wir sie auf den Luftwegen finden, unbedeutend ist.

Versuchen wir es trotzdem zu bewerten.

Konvergenz der Meridiane

Wir nennen die Konvergenz der Meridiane die Differenz zwischen dem Rv am Anfang eines Orthosegments und dem Rv am Ende desselben Segments.

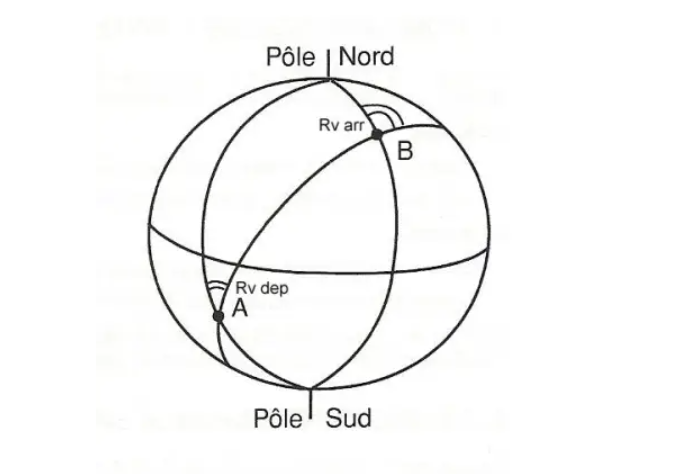
Dieser Unterschied wird in diesem Diagramm deutlich. Der Wert dieser Konvergenz kann mit der folgenden Formel ermittelt werden:

Conv = ∆ G x sin Lm

In dieser Formel stellt Delta G den Längenunterschied zwischen A und B dar und Lm ist der Durchschnitt ihrer Breiten.

Wir sehen sofort, dass die Konvergenz sehr schwach sein wird, wenn der Längengradunterschied klein ist (oder sogar Null auf einem Meridian, wie bereits gesehen). Bei einer Ost-West-Reise oder umgekehrt wird es hingegen das Maximum sein.

Wenn der mittlere Breitengrad niedrig ist, ist auch die Konvergenz niedrig. In äquatorialen Regionen ist der Großkreis also praktisch eine Loxodrome und umgekehrt!

Aus dieser Formel können wir also ableiten, dass die Konvergenz für Straßenabschnitte im Großkreis auf einem ziemlich hohen mittleren Breitengrad und mit einem signifikanten Längengradunterschied signifikant sein wird.



Givry-Fix

Der per Definition konstante Rv der Rhumb-Linie, die dieselben beiden Punkte verbindet, ist in erster Näherung der Durchschnitt der beiden wahren Abfahrts- und Ankunftsrouten des entsprechenden Ortho. Die Differenz des Rv loxo zum Rv-Abgang des ortho beträgt daher die Hälfte der Konvergenz.

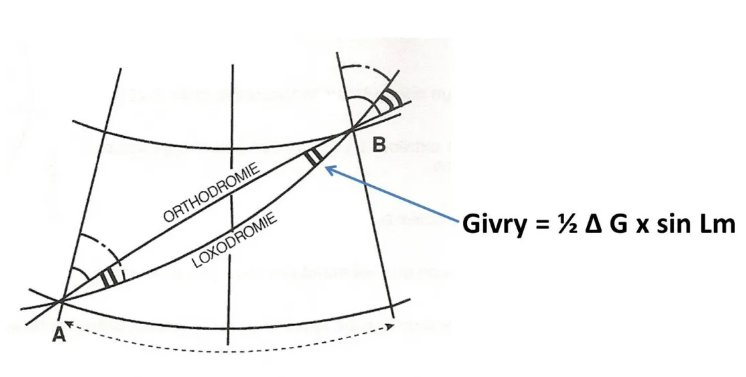
Dieser Wert, auch Givry-Korrektur genannt, benannt nach dem Hydrografen, der ihn erstellt hat, ermöglicht es beispielsweise, den Umriss eines Großkreises auf einer Mercator-Karte zu zeichnen.



Spitzname Givry

Ebenso gibt es einen „Pseudofrost“, der es ermöglicht, auf einer Lambert-Karte den Unterschied zwischen der Orthodromie und der geraden Kartenlinie auszuwerten.

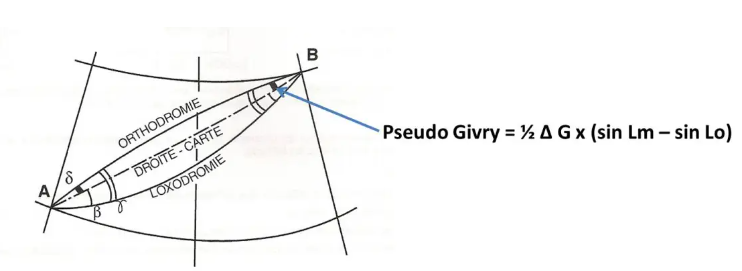
Mit dieser, da stimme ich zu, etwas komplizierten Formel können wir vor allem zeigen, dass, wenn sich die Straße in der Nähe der Tangentialparallele Lo befindet, die Differenz der Sinuswerte praktisch Null ist und daher auch der Pseudofrost, was uns das sagen lässt dass die richtige Karte praktisch ein Großkreis ist.

Die Tangentialparallelen einer Lambert-Karte oder die Standardparallelen einer Sekanten-Lambert-Karte werden so gewählt, dass die Karte in der dargestellten Region praktisch orthodromisch ist.

Die Elemente einer Rhumb-Linie, Rv und Entfernung sind zwar auf einer Mercator-Karte leicht zu messen, ihre genaue Berechnung ist jedoch recht kompliziert. Umgekehrt ist es nicht einfach, die Orthodromie auf einer Karte mit großer Präzision darzustellen und daher zu messen, sie ist jedoch recht einfach zu berechnen, dank der sphärischen Trigonometrie in einem Positionsdreieck, Rv-Abfahrt und -Ankunft und Großkreisentfernung. Da es sich dabei auch um die direkteste Route handelt, ist es nicht verwunderlich, dass uns moderne Navigationscomputer große Kreise folgen lassen!

Bewerbungsübung



Zum Abschluss und um das Ganze ein wenig zusammenzufassen, biete ich Ihnen eine kleine Bewerbungsübung an.

Sie nehmen einen Flug im großen kanadischen Norden, der Sie entlang der Ost-West-Route führt, die senkrecht über die Resolute Bay führt. Hier wird auf einer polaren stereografischen Karte der Straßenabschnitt dargestellt, auf dem Sie sich befinden (zum Vergrößern anklicken).

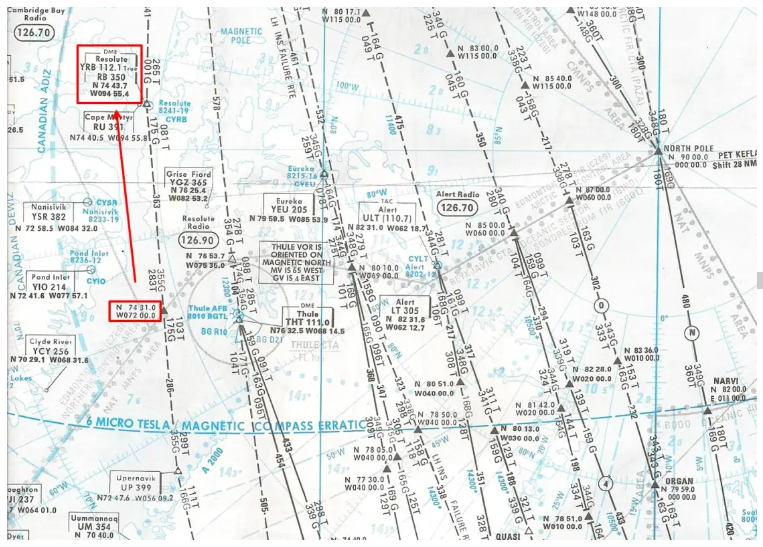
Ja, eine Ost-West-Straße, die durch eine fast vertikale Linie dargestellt wird, ist nicht sehr verbreitet!!! An die polare stereografische Karte muss man sich gewöhnen…

Die Konvergenz der Meridiane ist sehr wichtig, da, wie auf der Karte zu sehen ist, der Abfahrts-Rv in diesem Segment 283° (283T) beträgt und der Rv der Route, der in Resolute Bay ankommt, 261° beträgt (Umkehrung von 081T, der in der als Rv-Abfahrt angegeben ist). entgegengesetzten Richtung). Nicht weniger als 22°, ein Ergebnis, das auch rechnerisch verifiziert werden konnte, indem der Längengradunterschied, etwa 23°, mit dem Sinus der mittleren Breite, etwa 75°, multipliziert wurde.

In dieser Polarregion, in der die horizontale Komponente des Erdmagnetfelds sehr schwach ist, weniger als 6 Mikrotesla, haben Sie Ihren Kompass auf den wahren Norden eingestellt.

Sie haben den Punkt N74°31.0 W072°00.0 eine ganze Weile passiert und kurz nach dem Überqueren der 080W beginnen Sie, die VORDME von Resolute Bay, YBR zu empfangen. Dieses ist, wie die anderen kanadischen VORs in der 6-Mikrotesla-Zone, auf den wahren Norden eingestellt (True wird neben der Frequenz angezeigt).

Sie lesen einen QUJ, das wahre Äquivalent des QDM von 261° (oder in Näherung echte radiale 081°). Sind Sie auf der geplanten Route?

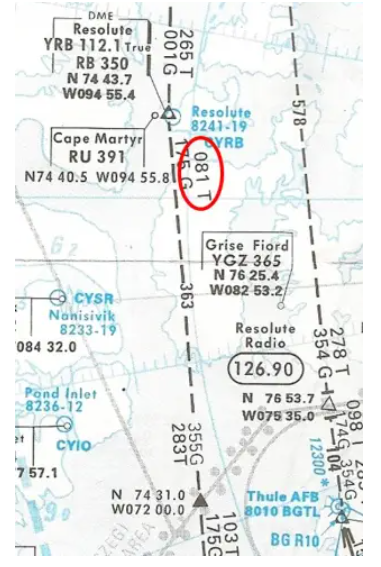
Ja, da der Start-Rv dieses Abschnitts, umgekehrt betrachtet, 081T ist, wie auf der Karte angegeben. Die VOR-Radiowellen bewegen sich in einer geraden Linie, das Flugzeug befindet sich tatsächlich auf dem Großkreis, bei dem Rv bei YBR 261° ankommt.

An diesem Punkt entscheiden Sie sich, das Flugzeug mit der Hdg Sel-Funktion zu steuern. Der Wind ist Null.

Wenn Sie den Kurs 261° anzeigen, folgen Sie dann dem wahren radialen 081°-Einflug? Um ihm zu folgen, benötigen Sie einen stärkeren oder schwächeren Kurs?

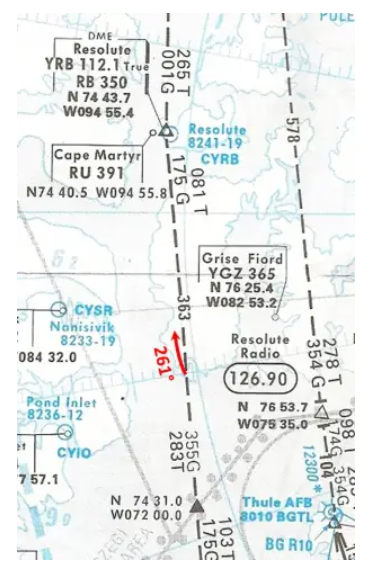
NEIN. Wenn wir den wahren Kurs von 261° konstant halten, fliegt das Flugzeug südlich der Route. Um der geplanten Route zu folgen, müssten wir einen stärkeren Kurs einschlagen…

Zum Zeitpunkt der Umstellung auf Hdg Sel betrug der Cv 272°. Wenn Sie so bleiben, fliegen Sie dann über die Resolute Bay? Wenn nicht, was muss getan werden?

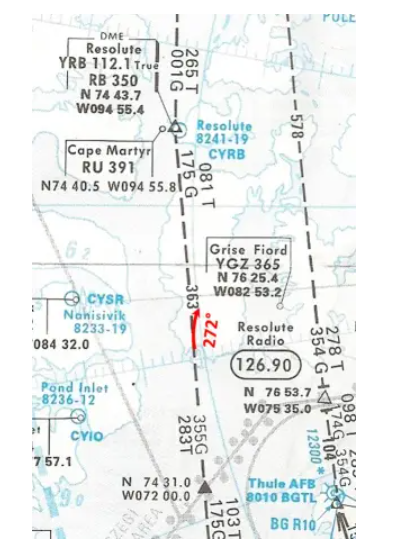
NEIN. Wir werden Resolute Bay nicht überfliegen, da das Flugzeug bei konstantem Kurs von 272° nördlich der Route fliegen wird. Um dem Radial zu folgen, wäre es notwendig, den Kurs schrittweise zu verringern, um bei YRB 261° zu erreichen.

Wenn Sie vom vorherigen Punkt N74°31.0 W072°00.0 bei konstantem Rv nach Resolute Bay wollen, welchen Kurs hätten Sie anzeigen müssen (kein Wind)?

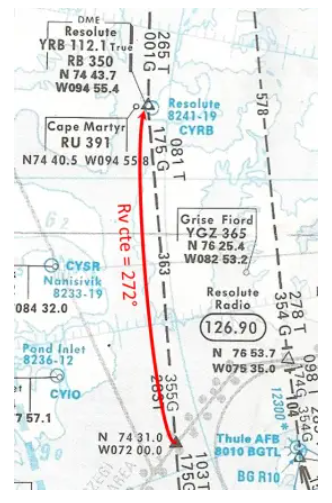
Der konstante RV ist der Durchschnitt des Abflug-RV und des Ankunfts-RV:

(283 261)/2 = 272°

Das gleiche Ergebnis erhalten wir, wenn wir die Givry-Korrektur auf den Abgang Rv anwenden:

g = ½(23 x sin 75°) = 11°

Rv cte = 283 – 11 = 272°

WÄHLEN SIE EINE ROUTE

Es bleibt nun die Wahl zwischen Orthodromie oder Rhumblinie. Wie wir bereits gesehen haben, wird diese Wahl nur auf einer langen Reise eine gewisse Bedeutung haben, und dies umso mehr, wenn der Ost-West-Trend signifikant ist.

Wie geht das? Für Betreiber von Verkehrsflugzeugen, die sehr treibstoffhungrig sind, ist die sogenannte RTM (Minimum Time Route) die ideale Route.

Ohne Wind ist RTM ein großer Kreis. Aber es ist illusorisch zu hoffen, einen langen Flug zu schaffen, ohne den geringsten Wind zu spüren ...

Es gibt eine grafische Methode, um anhand der vorhergesagten Winde die RTM zu ermitteln. Dies wurde in der Vergangenheit von Hand erledigt und war die Aufgabe von Einsatzkräften oder anderen Disponenten.

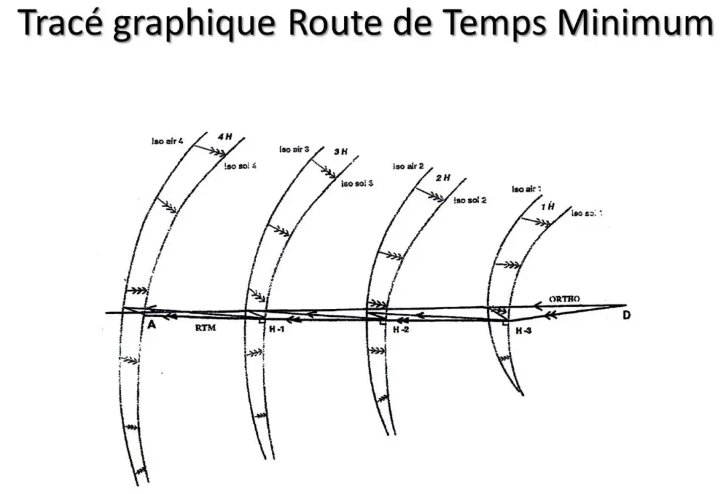
Heute verfügen sie über eine Software, deren Rechenleistung es ermöglicht, alle möglichen Routen in wenigen Augenblicken auszuwerten ...

Leider verfügen wir für unsere simulierten Flüge nicht über ein solches Tool, aber bestimmte Software liefert ein ziemlich ähnliches und sehr akzeptables Ergebnis.

All dies wird in den folgenden Artikeln besprochen …



ABSCHLUSS

Dieser erste Teil des Navigationsstudiums legt die Grundlagen, die es uns ermöglichen, besser zu verstehen, wie die Navigation auf einem Langstreckenflug praktiziert wird.

In den nächsten Artikeln befassen wir uns mit den verschiedenen Navigationsmitteln, wie Flugpläne entwickelt werden und wie ein Langstreckenflug abläuft.

Genießt alle die Flüge.