
Tan pronto como el hombre busca viajar, ya sea a pie, a caballo, en coche, en barco o en avión, el primer problema que se plantea es elegir la ruta a seguir. No es muy complicado si el trayecto es corto, conoces bien el terreno y tienes numerosos puntos de referencia. El problema se complica si queremos llegar muy lejos, cruzar un océano o un desierto, si es de noche o volamos sobre una capa de nubes. Este es el propósito de la navegación, cuyos conceptos básicos estudiaremos aquí…
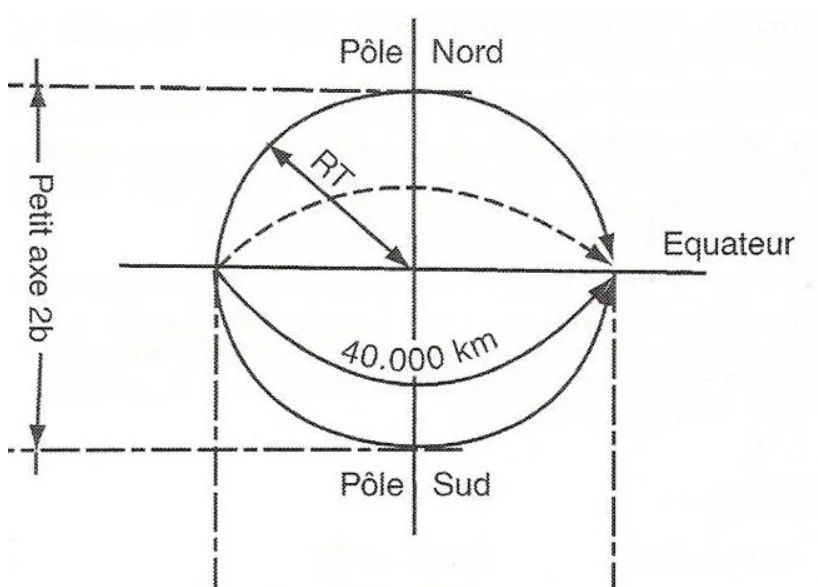
Nuestra Tierra es un elipsoide de revolución comparable, para simplificar, a una esfera con un radio medio de 6337 km. La diferencia entre el eje menor y el eje mayor es de aproximadamente 22 km, el perímetro medio se acerca a los 40.000 km.
La terre tourne sur elle-même, autour de son axe Nord Sud, en 24 heures, et autour du soleil en 365 jours. L’axe des pôles est incliné de 23°27’ par rapport au plan de l’écliptique, ce qui est à l’origine des saisons.
Para permitir la identificación de posiciones se han diseñado diferentes sistemas. El más conocido y común es el que, gracias al ecuador, separa la Tierra en dos hemisferios. Paralelo a este ecuador se definen paralelos que definen la latitud L. Se cuenta de 0° a 90° hacia el Norte o hacia el Sur.
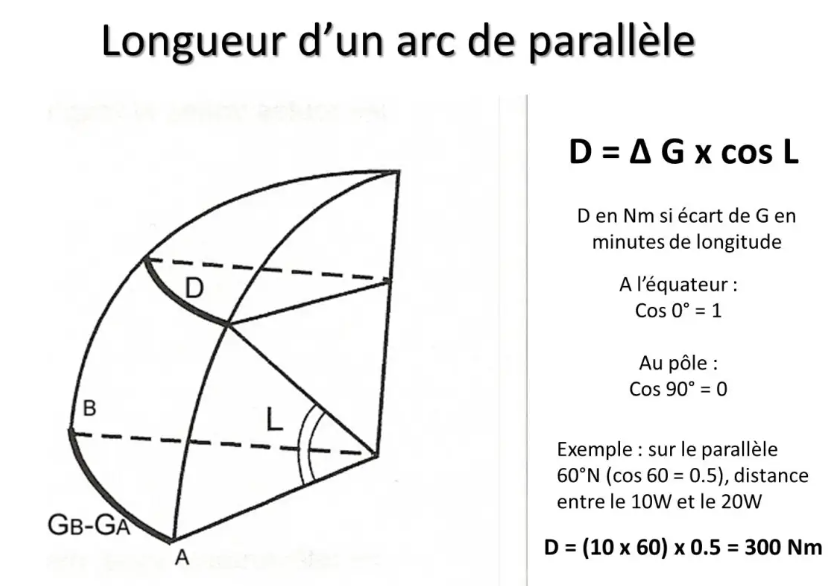
Para los matemáticos, y sin entrar en una demostración matemática compleja, con simplemente recordar que el coseno de la latitud disminuye de 1 a 0 cuando aumenta de 0° a 90°, intuitivamente recordaremos que la longitud de un arco de paralelo varía según al coseno de su latitud...
L'ESTIME (estimación)
C’est la base de toute navigation. Et c’est toujours d’actualité puisque les moyens de navigation les plus modernes ne font rien de plus mais avec la grande précision que permet la technologie actuelle, nous en reparlerons quand nous nous intéresserons à ces outils.
Quelque soit notre moyen de transport, pour aller au point B en partant du point A, il faut commencer par diriger, ou orienter notre véhicule vers le point B. C’est le plus important mais ce n’est pas forcément le plus simple : rappelons nous de Christophe Colomb parti cap à l’ouest pour aller aux Indes…!
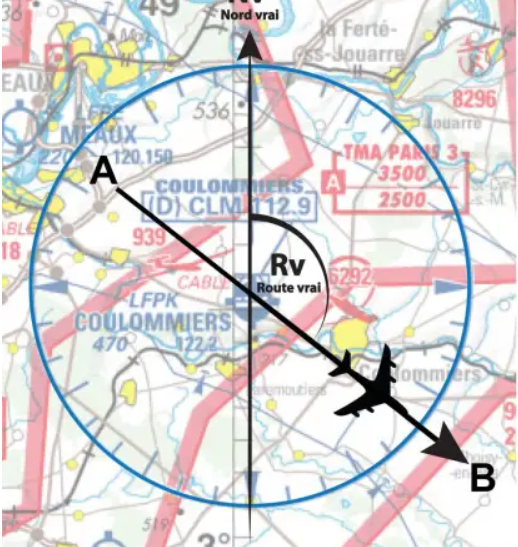
Por lo tanto, debemos poder decir en qué dirección se encuentra B y con respecto a qué referencia, generalmente la dirección del Polo Norte. Este es el ángulo de rumbo verdadero Rv, expresado en grados relativos a Nv, en el sentido de las agujas del reloj.
Si vemos B de A, ¡es fácil pero es raro! Podemos ir de un punto visible a otro, esto es lo que hacemos en vuelo visual. Si esto no es posible, o si quieres controlar la navegación visualmente, tendrás que medirla en un mapa o calcularla…
Luego necesitarás saber la distancia a recorrer para llegar al punto B, o un punto intermedio si se ha definido alguno. Luego podemos estimar el tiempo de vuelo para completar este viaje dividiendo esta distancia por la velocidad relativa al suelo.
El ángulo de rumbo Rv y el tiempo de viaje serán los dos elementos que nos permitirán navegar “a estima”. También decimos “cabeza y mira”.
Entre los medios más comúnmente utilizados para determinar los dos elementos de la navegación a estima, que son el ángulo de rumbo y la distancia, se encuentran, por supuesto, los mapas.
CARTOGRAFÍA
Muchas razones, incluida la navegación, llevaron a querer representar la Tierra. Pero es muy difícil hacerlo fielmente, en particular por su forma poco… católica (cf. Galileo y Copérnico)!
La representación más fiel es el mapamundi: evidentemente a gran escala, ¡y realmente poco práctico para utilizarlo en un avión!
General
Pour les cartes, représenter un objet vaguement sphérique sur une feuille de papier plate n'est pas possible avec précision : il faudra donc faire des compromis, et choisir quels sont les éléments à reproduire fidèlement au détriment d'autres qui le seront moins voire pas Para nada !
Para la navegación, uno de los puntos más importantes, como acabamos de ver, es la orientación de la trayectoria con el ángulo de la carretera Rv.
Conformidad
Por tanto, debemos poder medir los ángulos con precisión: esto es lo que llamamos conformidad. En un mapa conforme, si dos líneas se cruzan en un ángulo de 47° en la Tierra, sus representaciones en el mapa también se cruzarán en un ángulo de 47°. Por tanto, los ángulos se conservan.
Para que un mapa sea compatible, la escala alrededor de un punto determinado del mapa debe ser constante en todas las direcciones y, en particular, en las dos direcciones perpendiculares que son meridianos y paralelos.
¿Por qué es tan importante medir los ángulos con precisión?
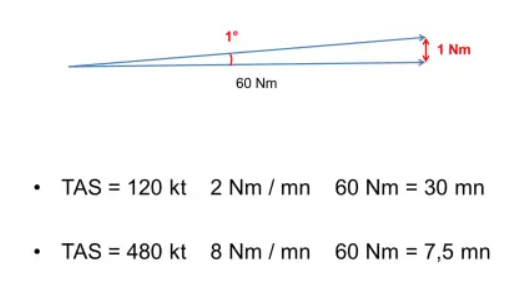
¡Con un pequeño error, después de 60 Nm la desviación de la carretera es de 1 Nm! Y 60 Nm son 30 minutos en el C172, ¡pero apenas 8 minutos para un Jet en crucero! Y existen múltiples fuentes de error: medición, error de los instrumentos de navegación, deriva del viento, etc.
la tarjeta correcta
Entonces, sería bueno que trazando una línea en el mapa con una regla definamos la trayectoria que queremos seguir, ortodrómica, lambda u otra “dromo”, volvemos a eso.
Equidistancia
Y por último, para medir distancias, si la escala fuera constante en todo el mapa (entonces diríamos que es equidistante), ¡sería perfecto! De hecho, como acabamos de ver, esto no supone un gran problema sabiendo que siempre podemos medir una distancia señalándola en el meridiano más cercano y contando los minutos de latitud, es decir, millas náuticas.
Tener estas tres cualidades con precisión es imposible: las cartas aeronáuticas, por tanto, serán las primeras en cumplirlas. Por lo demás, tendrás que elegir el compromiso más adecuado.
EN CARTA MERCATOR
Desarrollada en 1569 por Gerardus Mercator, quien le dio su nombre, es sin duda la representación más conocida del mundo.
Características
Es una proyección cilíndrica tangente al ecuador. Sin embargo, no es una proyección geométrica: el espaciado de los paralelos se calcula matemáticamente para que el mapa sea compatible y, por tanto, utilizable en la navegación (latitudes crecientes, primitiva de 1/cos L).
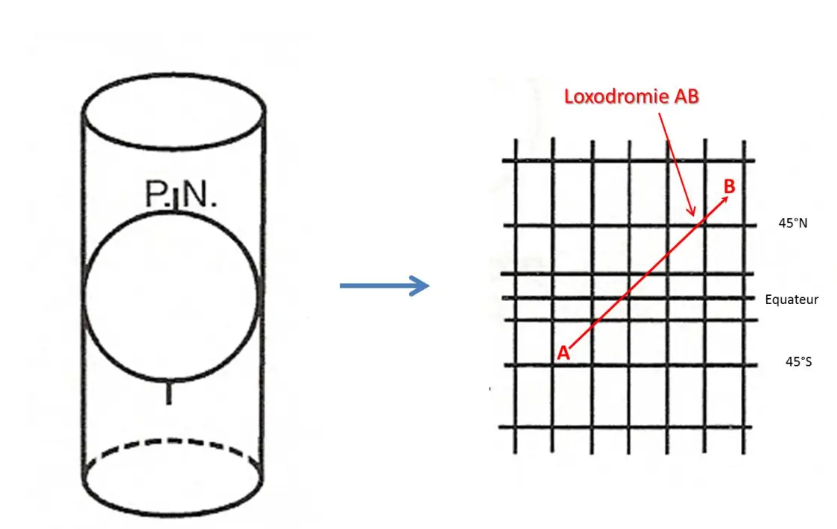
Los paralelos y meridianos se representan mediante líneas rectas perpendiculares entre sí: esto es muy práctico para navegar con rumbo constante porque si trazamos una línea en el mapa, el Rv es el mismo en todo el recorrido: el recorrido así trazado se llama línea de rumbo.
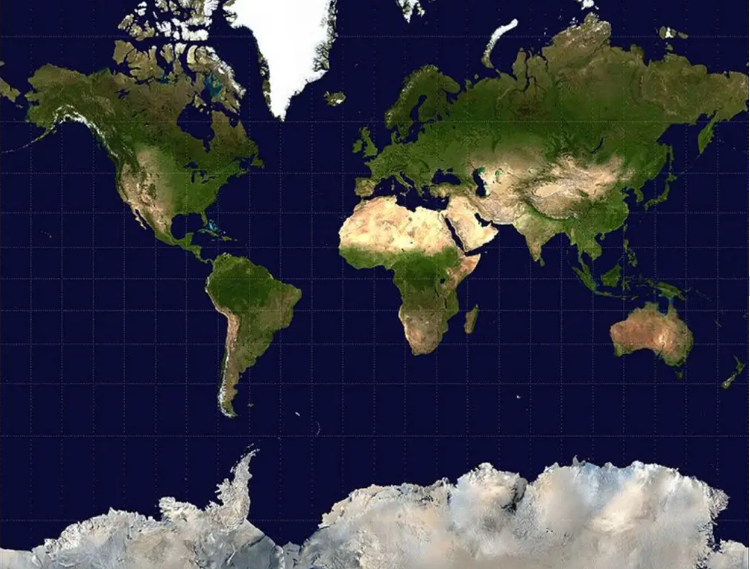
La escala, por el contrario, es muy variable, lo que distorsiona considerablemente las superficies: ¡¡¡Groenlandia, con sus 2 millones de km², parece tan vasta como toda África, que es aproximadamente 15 veces más grande!!!
La escala es mínima en el ecuador y aumenta hacia los polos.
No es posible representar las zonas polares en un mapa de Mercator.
La ruta de París a San Francisco que se muestra en los planisferios de las aerolíneas hace un hermoso circuito sobre Groenlandia y la Bahía de Hudson en Canadá, mientras que la línea recta pasaría sobre Nueva York. Quienes hayan tenido la oportunidad de volar a la costa oeste de Estados Unidos pueden confirmar que efectivamente estamos sobrevolando el gran Norte.
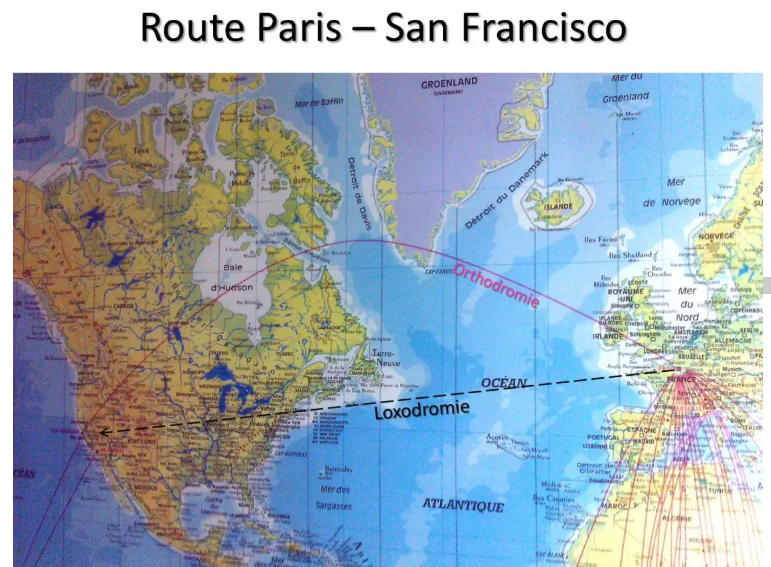
De hecho, la línea de rumbo no es la ruta más directa: la línea recta en nuestra Tierra esférica es en realidad un arco de círculo máximo (cuyo centro es el de la Tierra) que pasa por nuestros dos puntos A y B. Para tener confirmación, en un mapa mundial, al tender un cable entre París y San Francisco materializaremos la ruta más corta. Esto se llama ortodromía.
Para que os hagáis una idea, la distancia del círculo máximo entre CDG y SFO es de 4836 Nm mientras que la distancia loxodrómica ronda los 5600 Nm: 800 Nm, ¡¡¡la diferencia no es pequeña!!!
Construir un mapa de Mercator precisamente es una cuestión de profesionales: gracias IGN. Por otro lado, podemos construir fácilmente una pequeña parte gráficamente.
Construyendo un mapa de Mercator
Para ilustrar esto, te ofrezco un pequeño ejercicio práctico:
Imaginemos que heredas de tu abuela una buena suma de dinero y un gran terreno ubicado en el suroeste, alrededor de 45°N y 1°30 E. Con el dinero decides comprar un avión ultraligero, y con el terreno para hacer un track para usarlo… Quieres convertirlo en el mapa VAC, tanto para conocer el QFU y la longitud del track, como también para darlo a conocer a otros usuarios.
Primero dibuja un rectángulo de 12 cm de alto y 14 cm de ancho. Los lados verticales serán los meridianos, los horizontales los paralelos de nuestro mapa de Mercator.
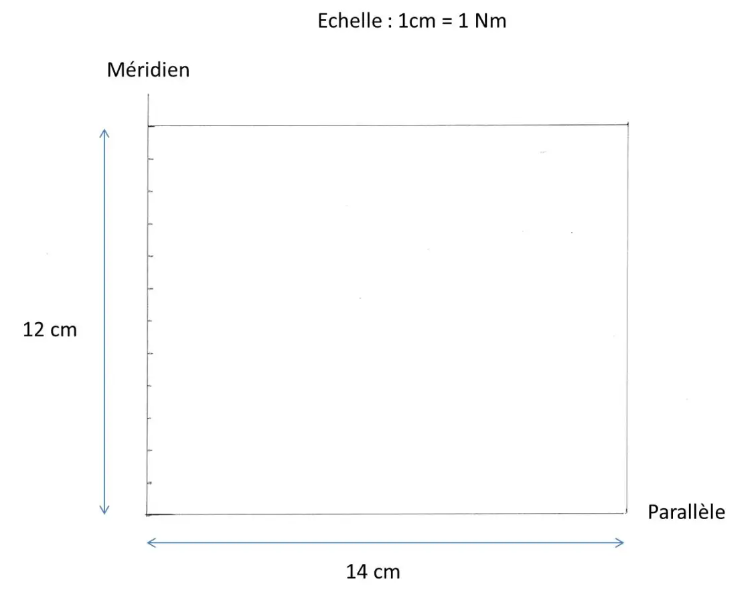
Escale el lado vertical izquierdo de cm a cm. Pondremos la escala: 1 cm = 1 Nm.
Dibuja una línea que parta de la esquina inferior izquierda, y que forme un ángulo de 45°, la latitud de nuestro terreno, con el paralelo inferior. También podemos hacer esto dibujando la diagonal de un cuadrado...
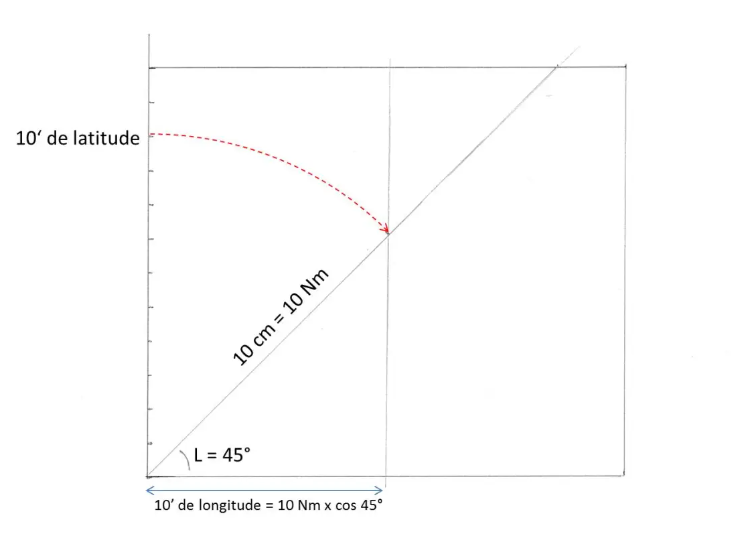
Sobre esta línea, trasladar el meridiano de 10 cm que representa 10 minutos de latitud, es decir 10 Nm. Bajar una línea vertical hasta el paralelo inferior. Acabamos de delimitar la longitud de un segmento de 10 minutos de longitud: como vimos arriba, mide 10 x cos 45° o aproximadamente 7 Nm, por lo tanto 7 cm en nuestro mapa. (cos 45° = 0,707, como el seno, ¡¡¡el más aerodinámico de los senos!!!).
Por tanto, la escala es la misma en el meridiano y en el paralelo: ¡nuestro lienzo es, por tanto, coherente!
Entiendes mejor por qué elegí un rectángulo de 14 cm de ancho… que por tanto representa 20 minutos de longitud.
Ya sólo queda graduar nuestra escala de longitud cada 7 mm.
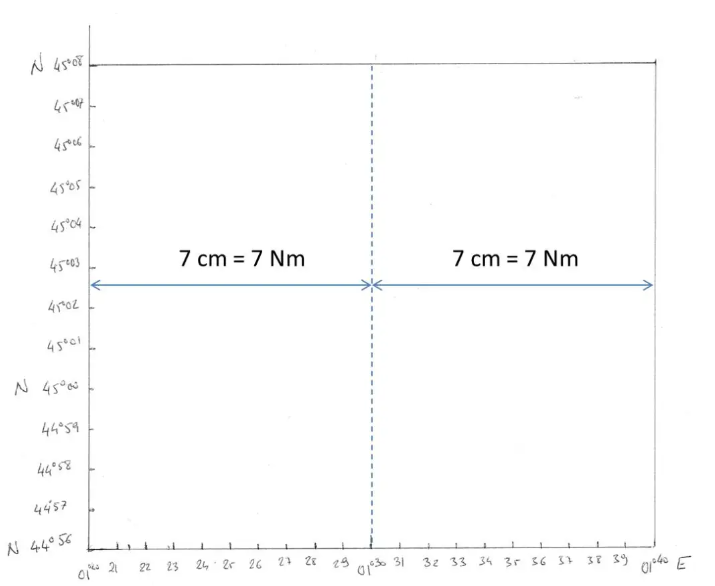
Pour avoir notre piste à peu près centrée, on va chiffrer les latitudes de 44°56’ à 45°58’N, et les longitudes de 001°20’ à 001°40’E.
Acabamos de crear un lienzo consistente (misma escala en los meridianos y paralelos). ¡¡¡Es un lienzo de Mercator ya que los meridianos y paralelos son líneas perpendiculares!!!
Con tu GPS fuiste a medir la posición de las dos QFU: al NO: 45°02.6 N y 001°28.3 E y al SE 45°02.2 N y 001°29.8 E. Solo queda posicionarlos en nuestro mapa. .
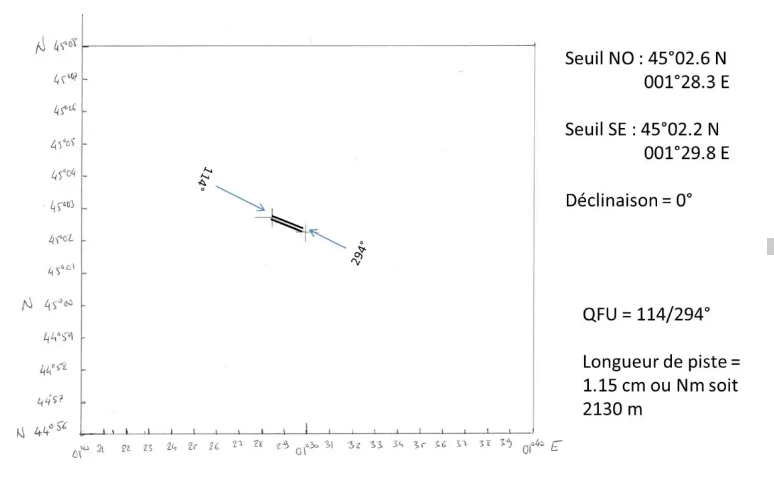
Con un transportador ahora se puede medir el QFU, y con un doble decímetro la longitud de la vía: encontré, por mi parte, el QFU 114°/294° y una longitud de vía de 1,15 cm, por lo tanto 1,15 Nm, o 2130 m. .
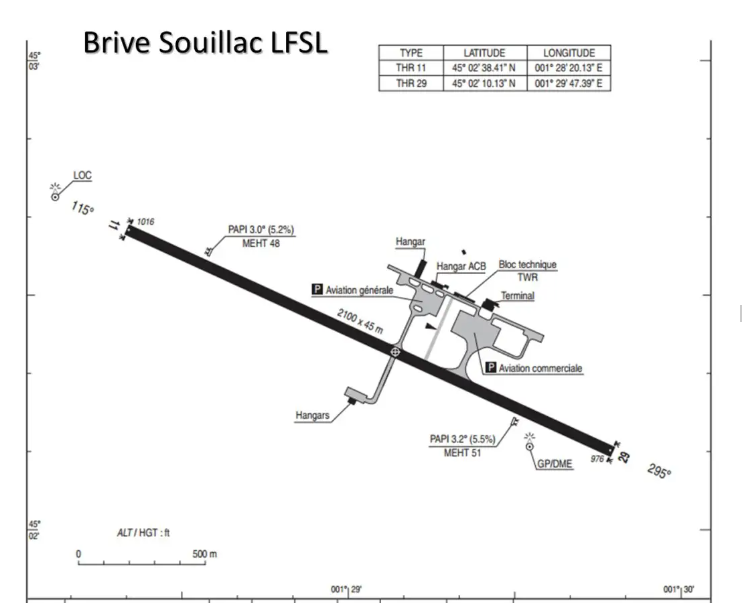
Indagando un poco en los archivos del SIA, descubrirá fácilmente que su abuela le dejó, efectivamente, las tierras de Brive Souillac, cuyos QFU son 115°/295° y la longitud de la pista es de 2100 m!!!
en aeronáutica
La proyección de Mercator rara vez se utiliza para cartas de navegación aeronáutica. Sólo las regiones ecuatoriales permitirán tener un mapa conforme, por supuesto, pero también prácticamente ortodrómico y equidistante, ya que está cerca del ecuador.
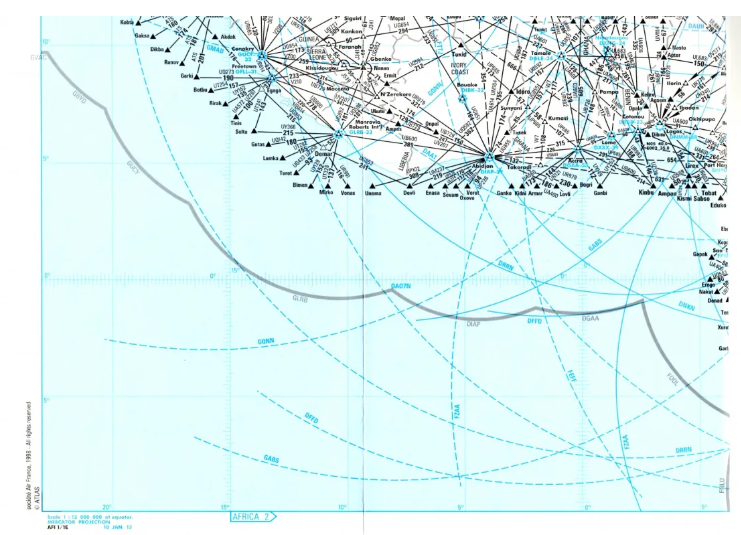
Esta hoja de ruta AFRICA 1 para la planificación de vuelos ETOPS es una de ellas, aunque en realidad no es un mapa de navegación (haga clic para ampliar).
LA TARJETA LAMBERT
Uno de los principales defectos del mapa de Mercator es que la línea recta en el mapa no representa la línea recta en la Tierra. Pero existen soluciones… la primera se llama tarjeta de Lambert.
Características
Presentada a finales del siglo XVIII por el matemático alsaciano Johann Henrich Lambert, se trata de una proyección cónica conforme que tangente a la esfera terrestre a lo largo de un paralelo. Como ocurre con el mapa de Mercator, no se trata de una proyección geométrica sino de una construcción matemática.
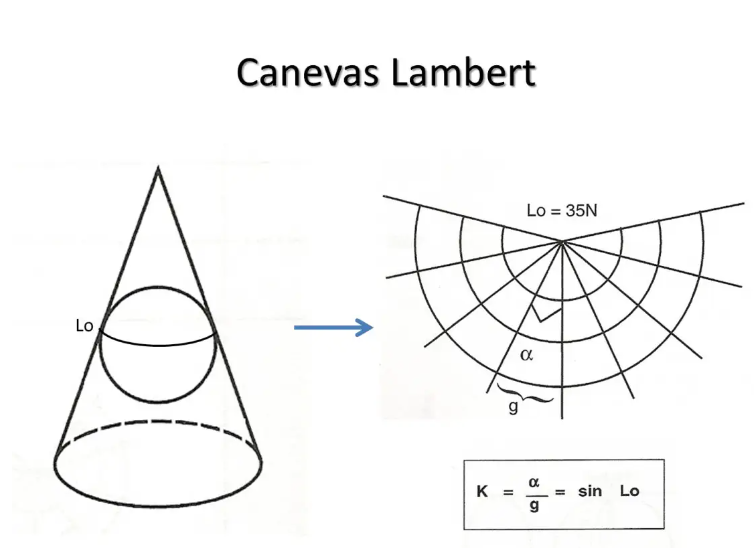
Los meridianos están representados por líneas rectas que convergen hacia el polo. Llamamos factor de convergencia K a la relación entre el ángulo que forman dos meridianos en el mapa y el ángulo que forman en la Tierra. Si el paralelo de tangencia es de latitud Lo, el factor K = sen Lo.
Los paralelos están representados por círculos concéntricos.
Como todos los mapas conformes, este tipo de mapas son prácticamente ortodrómicos cerca del paralelo de tangencia, es decir que el mapa recto es prácticamente la representación de un ortodrómico. ¡El mapa de Mercator es, de hecho, un caso especial del mapa de Lambert donde el paralelo de tangencia es el ecuador! Por tanto, será ortodrómico cerca del ecuador.
Por lo tanto, para tener un mapa ortodrómico de Lambert bastará con elegir un paralelo de tangencia centrado en el área que se desea representar...
Al igual que con el mapa de Mercator, la escala es mínima en el paralelo de tangencia Lo y aumenta significativamente a medida que nos alejamos de él.
Para remediar este inconveniente, se crearon los llamados mapas cónicos de Lambert “secantes”. La escala oficial del mapa sólo es real al nivel de dos paralelos situados a cada lado del paralelo de tangencia. Esto equivale a decir que el cono de proyección corta la superficie de la Tierra a lo largo de estos dos paralelos llamados “estándar” o “escala conservada”. La escala es ligeramente menor entre estos dos paralelos y un poco mayor más allá, lo que da un lienzo prácticamente equidistante sobre un área más grande.
El factor K es entonces el seno de la latitud media entre los dos paralelos estándar, o aproximadamente porque la variación de escala no es simétrica a ambos lados del paralelo de tangencia.
La mayoría de las cartas aeronáuticas utilizadas en nuestras regiones de latitudes medias son de este tipo. Así podemos leer en el mapa VFR a 1:500.000 del noroeste de Francia publicado por el IGN: “Proyección cónica conforme de Lambert. Paralelos de escala conservada 45°54' y 47°42'" (los paralelos estándar).
Esto hace que la latitud media Lo = 46°48' N y por lo tanto un factor K = 0,728.
en aeronáutica
Aquí, por ejemplo, un extracto del camión ATLAS 55C utilizado para cruzar el Atlántico Norte (aquí un vuelo París-Nueva York), y cuyos paralelos estándar son 37° y 65° N (haga clic para ampliar).
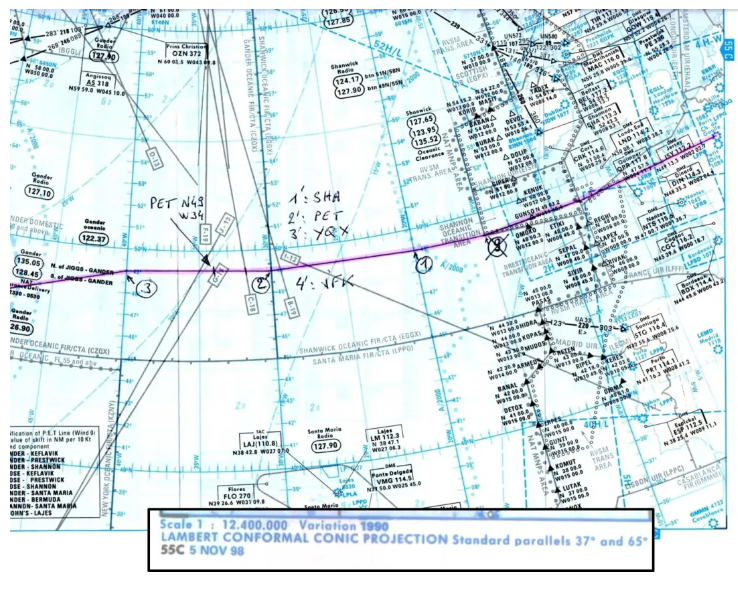
Podemos ver claramente los meridianos, representados por líneas rectas, que convergen hacia el Polo Norte, y los paralelos que están representados por círculos concéntricos.
Con este tipo de mapas estamos muy cerca del mapa perfecto: en la zona representada es consistente para medir con precisión rutas o rumbos, ortodrómico para trazar con una regla los recorridos más cortos, y prácticamente equidistante ya que la escala varía poco: el santo Grial del cartógrafo!
Curiosamente el mapa SIA "En ruta", aunque no está indicado, es un mapa de Mercator, lo cual es fácilmente comprobable con sus meridianos paralelos, a la vez que presenta vías aéreas definidas por radiales VOR, que son ortodromia???
*
¿Qué tipo de tarjeta?
Para cerrar este capítulo: intentemos determinar qué tipo de lienzo utiliza el SIA para presentar los SID y STAR: tomemos, por ejemplo, una de las tarjetas SID del LFPG.
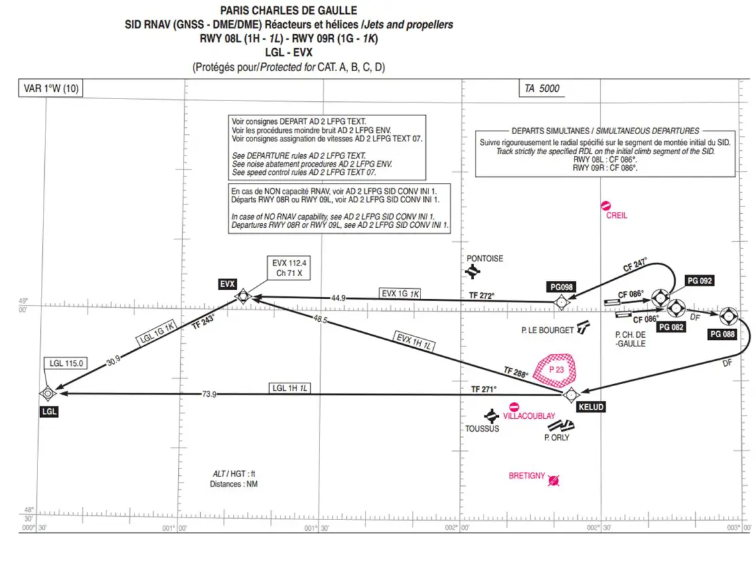
Con una regla o acercando un paralelo al borde de la pantalla, vemos que los paralelos representados no son líneas rectas. Y midiendo la distancia entre dos meridianos arriba y abajo vemos que no son paralelos.
Por tanto, no se trata de un lienzo de Mercator, ciertamente de Lambert, pero el pequeño tamaño de la pieza representada no permite medir el ángulo entre dos meridianos que habría que comparar con su diferencia de longitud para determinar el factor K y por tanto el paralelo de tangencia…
Para obtener más información sobre las tarjetas Lambert utilizadas en Francia, puede consultar la página de Wikipedia sobre las tarjetas Lambert:
https://fr.wikipedia.org/wiki/Projection_conique_conforme_de_Lambert
LES AUTRES TYPES DE CARTE
Con el mapa de Mercator para la región del ecuador y el mapa de Lambert para las otras latitudes resolvimos casi todos los problemas. Quedan algunos casos especiales que dieron lugar a la invención de tarjetas (muy) particulares.
El mapa estereográfico polar
El primero de estos casos es un mapa elaborado para representar las regiones polares: esto se llama lienzo estereográfico polar. Es una proyección sobre un plano tangente al polo. Y esta vez realmente podríamos construirlo mediante proyección geométrica desde el polo opuesto.
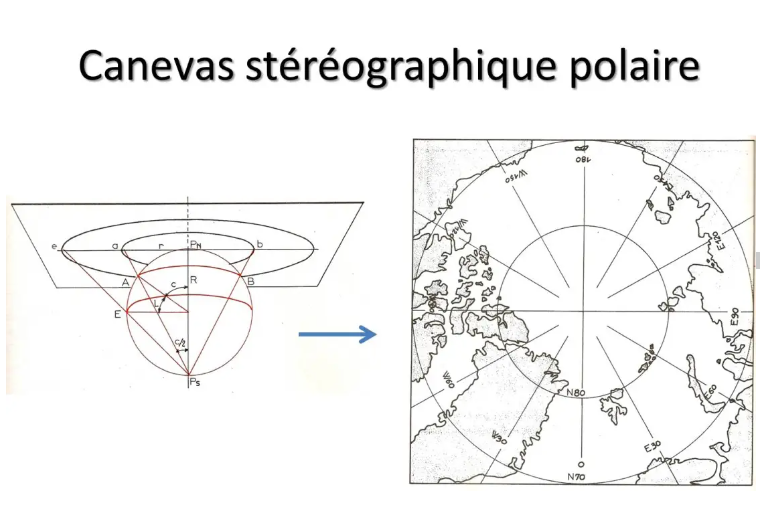
Esto nos da un mapa donde todos los meridianos están representados por líneas rectas que parten del polo en forma de rosa de 360°. Los paralelos son círculos concéntricos.
Este mapa, por supuesto, cumple con las normas para su uso en la navegación. Es ortodrómico cerca de su punto de tangencia, el polo.
La escala será mínima en el polo y aumentará al alejarse de usted.
Por tanto, su uso se limita a la representación de regiones polares y rutas asociadas. A continuación se muestra un extracto del vehículo de turismo polar ATLAS 90C:
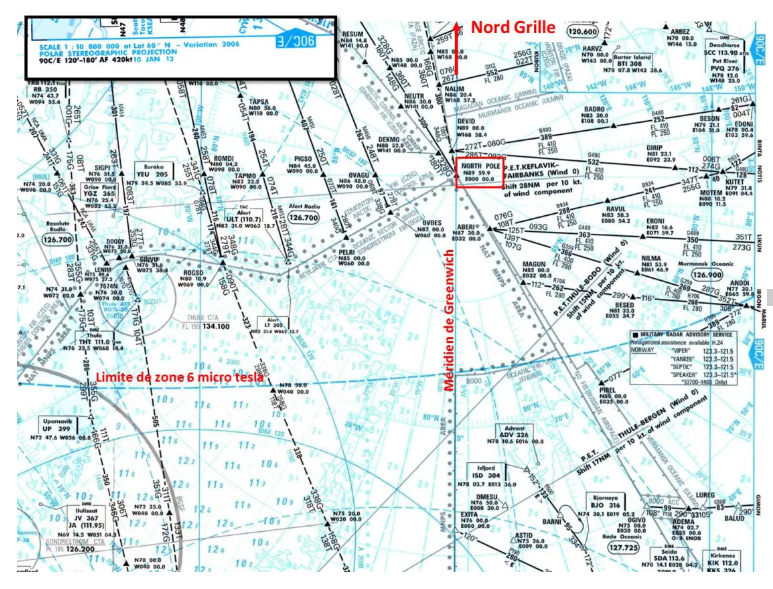
La fuerte convergencia de los meridianos y la falta de fiabilidad de las brújulas magnéticas en las regiones polares (zona 6 micro teslas) hacen muy difícil seguir una ruta con rumbo constante. Para esto, el mapa tiene una cuadrícula orientada siguiendo una Cuadrícula Norte para navegar a una Cuadrícula de Ruta Rg constante.
En el pasado se han imaginado y utilizado otros tipos de lienzos.
La carte Mercator Transverse
Partiendo de la idea de que el ecuador es un gran círculo, se diseñaron los llamados mapas transversales de Mercator siguiendo el mismo principio que el directo de Mercator, una proyección cilíndrica, pero teniendo como "ecuador" el meridiano de Greenwich y el meridiano de 180° (podemos hacerlo también según cualquier par de meridianos y su antimeridiano).
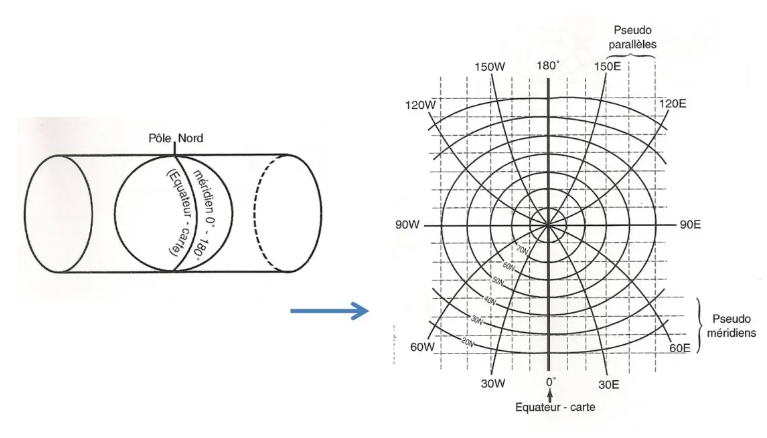
Esto da un lienzo que será conforme, por supuesto, y ortodrómico a cada lado de su ecuador cartográfico, que también será el único representado por una línea recta. Por lo tanto, es imperativo utilizar una cuadrícula con “pseudo paralelos” y “pseudo meridianos”…
C’est sur ce modèle qu’avait été faite la carte Air France « France-Alaska » utilisée avant l’arrivée des systèmes de navigation par inertie INS et pendant la guerre froide, période pendant laquelle le survol de la Sibérie étant interdit, la route la plus courte vers le Japon passait par la région du Pôle Nord.

¡Uso reservado a navegantes profesionales ya que son bastante difíciles de manejar…!
El mapa de Mercator oblicuo
Aún más claro, ¿por qué no hacer un mapa de Mercator con, para el ecuador del mapa, cualquier círculo máximo?
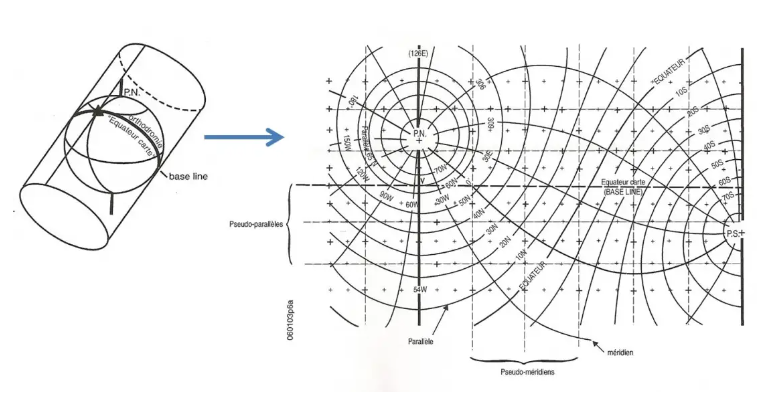
Esto se llama mapa Oblique Mercator, ¡¡¡y aún menos fácil de usar !!!
¿ORTODROMIA O LOXODROMIA?
Como vimos anteriormente, hay al menos dos trayectorias posibles entre un punto A y un punto B: la línea lomboidal y el círculo máximo.
Cuál elegir ?
Dependerá de diferentes elementos, y principalmente del medio de navegación que podremos utilizar.
La más simple, la brújula magnética, le permitirá seguir líneas de rumbo, con un rumbo constante, siempre que, por supuesto, sepa cómo corregir la desviación, la declinación y la deriva. Hablaremos de ello nuevamente en un artículo dedicado a los métodos de navegación.
Como también veremos en este artículo, lo moderno significa seguir grandes círculos... Por otro lado, seguir un gran círculo con una brújula no es muy fácil porque el Rv cambia todo el tiempo. ¡Y los medios de navegación modernos no pueden seguir una línea de rumbo!
¿Pero es muy importante marcar la diferencia?
En primer lugar, hay algunos casos en los que ambos se confunden: el ecuador es a la vez orto y loxo. Asimismo, los meridianos son ortos (medios círculos grandes) pero también loxos ya que los seguimos a Rv constante, ¡180° o 360°!
El caso general permanece. Digamos de entrada que en tramos de algunas decenas de Nm como los que encontramos en las vías respiratorias, la diferencia es insignificante.
Intentemos evaluarlo de todos modos.
Convergencia de los meridianos
Llamamos convergencia de los meridianos a la diferencia entre la Rv al inicio de un segmento orto y la Rv al final de este mismo segmento.
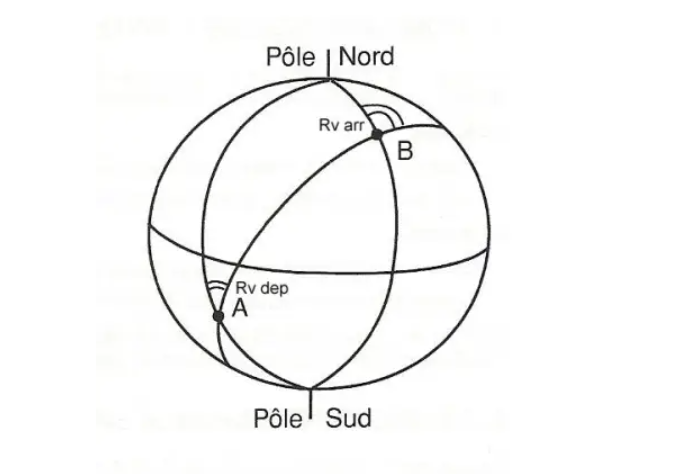
Esta diferencia aparece claramente en este diagrama. El valor de esta convergencia se puede evaluar mediante la siguiente fórmula:
Conv = ∆ G x sen Lm
En esta fórmula, delta G representa la diferencia de longitud entre A y B, y Lm es el promedio de sus latitudes.
Inmediatamente vemos que si la diferencia de longitud es pequeña, la convergencia será muy débil (o incluso cero en un meridiano como ya se ha visto). En cambio, será máximo para un trayecto Este/Oeste o viceversa.
Asimismo, si la latitud media es baja, también lo será la convergencia. Entonces, en las regiones ecuatoriales, el gran círculo será prácticamente una línea de rumbo y viceversa.
Entonces podemos deducir de esta fórmula que la convergencia será significativa para los segmentos de carretera de gran círculo en una latitud media bastante alta y con una diferencia de longitud significativa.
Arreglo de Givry
La Rv de la línea de rumbo, constante por definición, que conecta estos mismos dos puntos será, como primera aproximación, la media de las dos rutas verdaderas de salida y llegada del orto correspondiente. La diferencia del Rv loxo con la salida Rv del orto será por tanto la mitad de la convergencia.
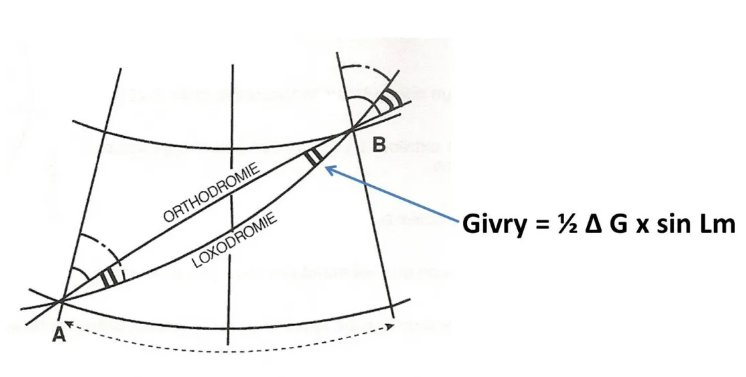
Este valor, también llamado corrección de Givry, en honor al ingeniero hidrográfico que lo creó, permite, por ejemplo, trazar el contorno de un gran círculo en un mapa de Mercator.
Apodo Givry
Del mismo modo, existe una “pseudo-helada” que permite evaluar, en un mapa de Lambert, la diferencia entre la ortodromía y la línea recta del mapa.
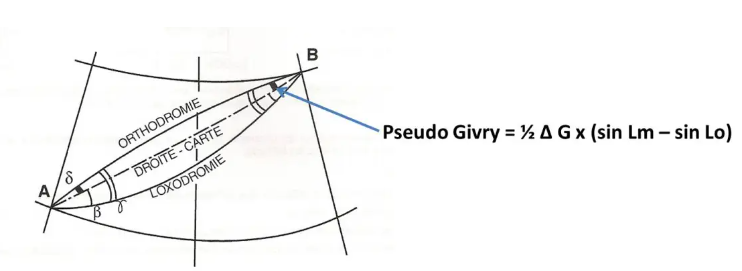
Esta fórmula, un poco complicada, estoy de acuerdo, nos permite sobre todo demostrar que si la carretera está situada cerca del paralelo de tangencia Lo, la diferencia de los senos es prácticamente nula, y por tanto la pseudo-helada también, lo que nos permite decir que el mapa correcto es prácticamente un círculo máximo.
El paralelo de tangencia de un mapa de Lambert, o los paralelos estándar de un mapa de Lambert secante, se elegirán de manera que, en la región representada, el mapa sea prácticamente ortodrómico.
Los elementos de una línea de rumbo, Rv y distancia, si bien son fáciles de medir en un mapa de Mercator, son bastante complicados de calcular con gran precisión. Por el contrario, la ortodromía no es muy sencilla de representar en un mapa con gran precisión y por tanto de medir, pero es bastante fácil de calcular, gracias a la trigonometría esférica en un triángulo de posición, la salida y llegada de Rv y la distancia del círculo máximo. Como también es la ruta más directa, no es de extrañar que los modernos ordenadores de navegación nos hagan seguir grandes círculos.
Ejercicio de aplicación
Para terminar y resumir un poco todo esto, te ofrezco un pequeño ejercicio de aplicación.
Está tomando un vuelo en el gran norte de Canadá, que le llevará por la ruta este/oeste que pasa verticalmente sobre Resolute Bay. Aquí está representado, en un mapa estereográfico polar, el tramo de carretera en el que se encuentra (haga clic para ampliar).
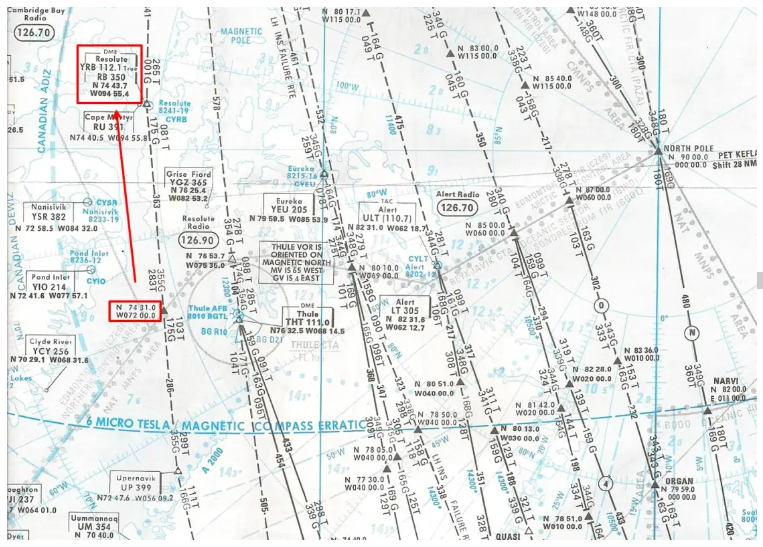
¡Sí, una carretera Este/Oeste representada por una línea casi vertical no es muy común! El mapa estereográfico polar, hay que acostumbrarse…
La convergencia de los meridianos es muy importante ya que, como se ve en el mapa, en este segmento la salida Rv es 283° (283T) y la ruta Rv llegando a Resolute Bay es 261° (inversa de 081T indicada como salida Rv en el direccion opuesta). Nada menos que 22°, resultado que también podría verificarse mediante cálculo multiplicando la diferencia de longitud, aproximadamente 23°, por el seno de la latitud media, aproximadamente 75°.
En esta región polar donde la componente horizontal del campo magnético de la Tierra es muy débil, menos de 6 microteslas, usted ha puesto sus brújulas en el Norte verdadero.
Ha pasado bastante tiempo por el punto N74°31.0 W072°00.0 y poco después de cruzar la 080W comienza a recibir el VORDME desde Resolute Bay, YBR. Este está configurado, como los otros VOR canadienses ubicados en la zona de 6 microteslas, en el Norte verdadero (Verdadero indicado al lado de la frecuencia).
- Estás leyendo un QUJ, verdadero equivalente del QDM de 261° (o verdadero radial de 081° en aproximación). ¿Estás en la ruta planificada?
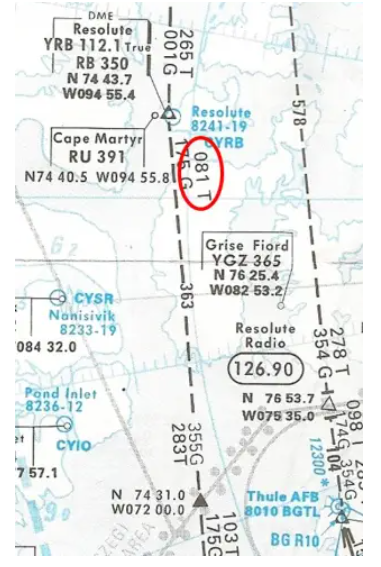
Sí, ya que la Rv inicial de este segmento, tomada al revés, es 081T como se indica en el mapa. Las ondas de radio VOR se mueven en línea recta, el avión está efectivamente en el círculo máximo en el que Rv llega a YBR 261°.
En este punto, decide guiar la aeronave con la función Hdg Sel. El viento es cero.
- Si muestra un rumbo de 261°, ¿seguirá el verdadero radial de 081° hacia adentro? Para seguirlo, ¿necesitaría un rumbo más fuerte o más débil?
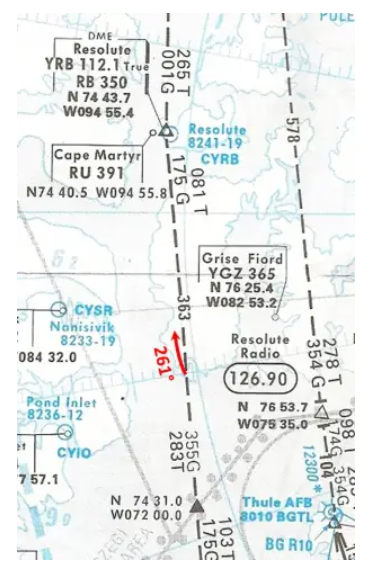
No. Si mantenemos constante el rumbo verdadero de 261°, el avión se dirigirá al sur de la ruta. Para seguir la ruta prevista, tendríamos que tomar un rumbo más firme…
- En el momento en que cambió a Hdg Sel, el Cv era 272°. Si te quedas así, ¿volarás sobre Resolute Bay? Si no, ¿qué habrá que hacer?
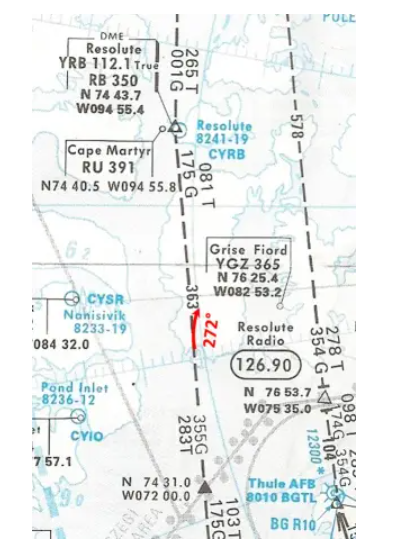
No. No sobrevolaremos Resolute Bay porque, al mantener un rumbo constante de 272°, el avión se dirigirá al norte de la ruta. Para seguir la radial sería necesario disminuir gradualmente el rumbo hasta llegar a 261° en YRB.
- Si, desde el punto anterior N74°31.0 W072°00.0 quisieras ir a Resolute Bay con Rv constante, ¿qué rumbo deberías haber mostrado (sin viento)?
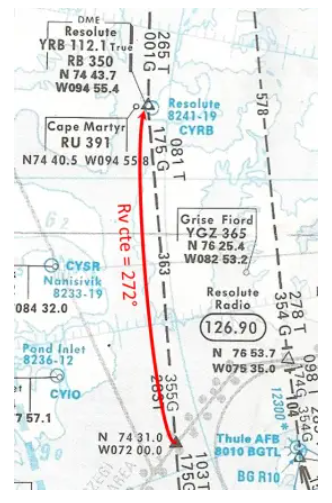
El RV constante será el promedio del RV de salida y el RV de llegada:
(283 261)/2 = 272°
Encontramos el mismo resultado aplicando la corrección de Givry a la Rv de salida:
g = ½(23 x sin 75°) = 11°
Rv cte = 283 – 11 = 272°
ELIGE UNA RUTA
Ahora queda elegir entre ortodromía o línea de rumbo. Como ya hemos visto, esta elección sólo tendrá cierta importancia en un viaje largo, y más aún si la tendencia este/oeste es significativa.
Así que ¿cómo se hace? Para los operadores de aviones de línea, que consumen mucho combustible, la ruta ideal es la llamada RTM (Ruta de Tiempo Mínimo).
Sin viento, RTM es un gran círculo. Pero es ilusorio pretender realizar un vuelo largo sin sentir el más mínimo viento...
Existe un método gráfico para encontrar, en base a los vientos previstos, cuál sería el RTM. Esto es lo que se hacía antiguamente, a mano, era trabajo de agentes de operaciones u otros despachadores.
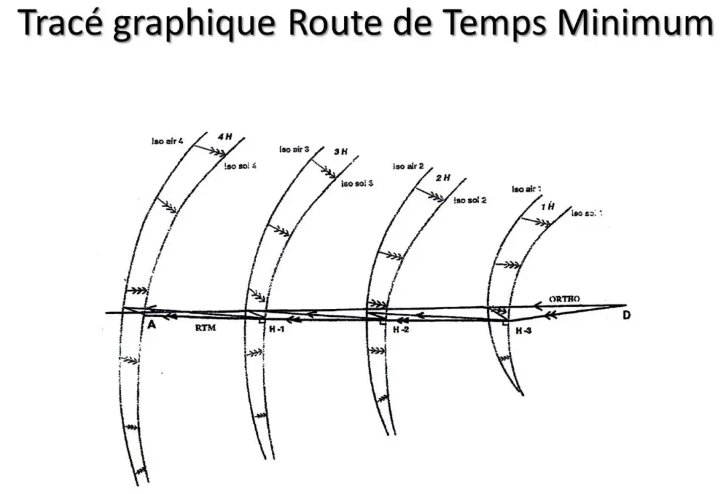
Hoy en día disponen de software cuya potencia de cálculo permite evaluar todas las rutas posibles en unos instantes...
On ne dispose malheureusement pas de ce genre d’outil pour nos vols simulés, mais certains logiciels donnent un résultat assez similaire et très acceptable.
Todo esto se tratará en los artículos siguientes...
CONCLUSIÓN
Esta primera parte del estudio de la navegación sienta las bases que nos permitirán comprender mejor cómo se practica la navegación en un vuelo de larga distancia.
En los próximos artículos estudiaremos los diferentes medios de navegación, cómo se elaboran los planes de vuelo y cómo se desarrolla un vuelo de larga distancia.
Disfruten todos los vuelos.



